The model describes the incompressible flow of immiscible fluids governed by the Navier-Stokes equations with jump conditions across the interfaces. The fluid interfaces are captured by a level-set method that handles topological changes so that surfaces can merge and break up. Thus, levelZ is used to study phenomena like coalescence (merging of droplets), bouncing, jetting and partial coalescence. Such phenomena are challenging to model and simulate correctly. Our model can capture the additional effects of both electric fields and surfactant covering, which is useful to study coalescence of water droplets in oil under the influence of electric fields. Furthermore, the numerical framework includes models for heat exchange and phase transition, and even models for more rigid droplet surface coverings such as asphaltenes. Complex geometries can be taken into account using a penalization method. Good qualitative agreement is achieved when comparing to experimental data and other literature studies.
Examples of studies enabled by the levelZ model are:
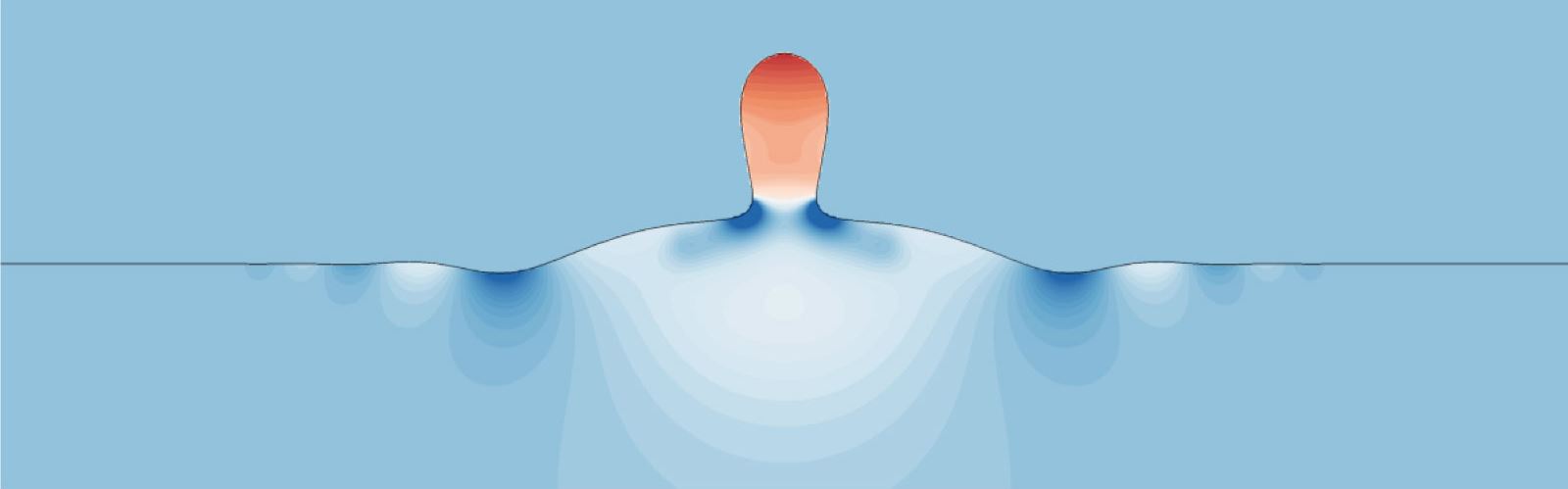
- Falling droplets impinging a liquid pool (see an example in the figure below)
- Simulations of head-on collisions with and without electric forces and surfactant covering
- Boiling (although restricted to the Boussinesq approximation for the density)
Fundamental knowledge of such processes is important for instance for design of heat exchangers in natural gas liquefaction plants, or for understanding electrocoalescence processes for separation of water and oil.
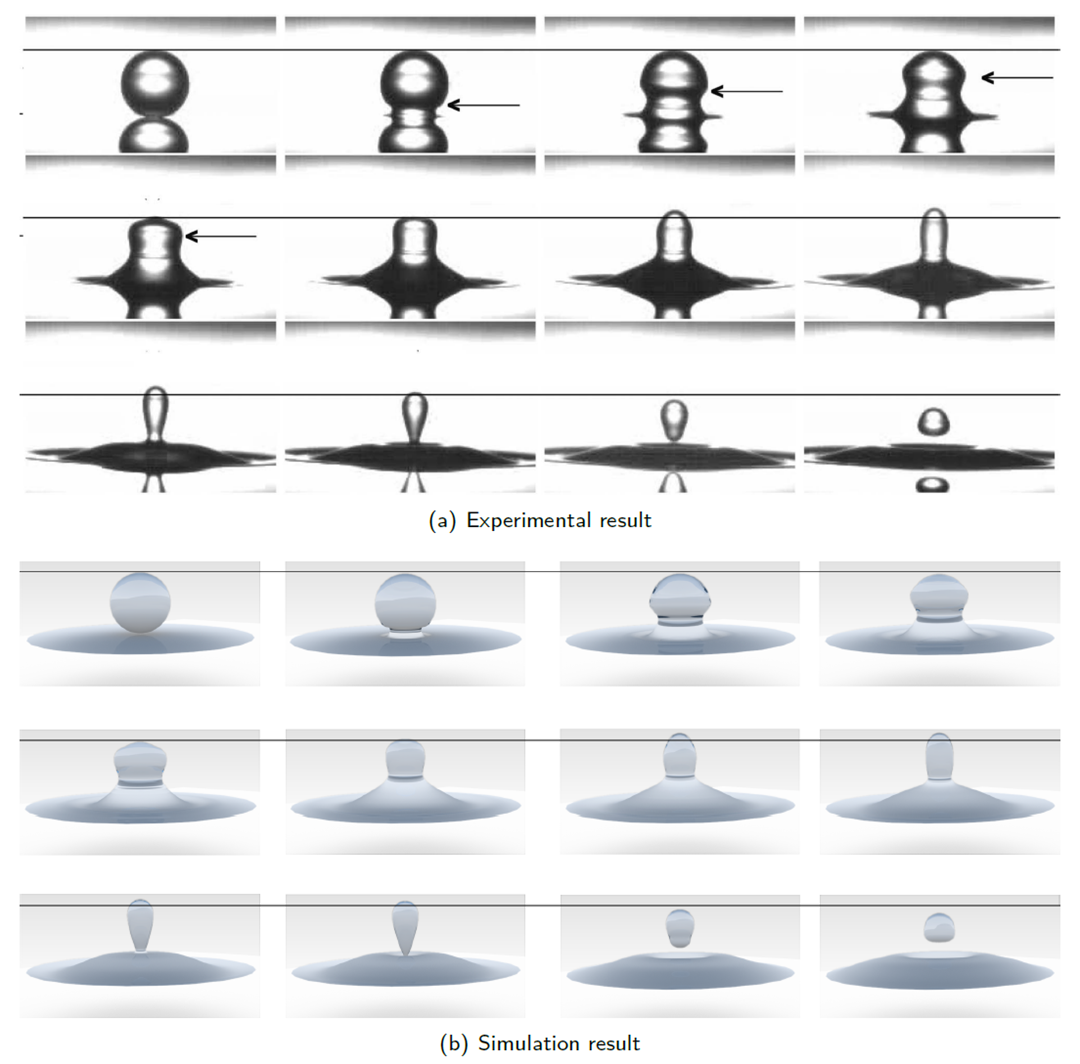
A 1.1 mm diameter water droplet merging with a water pool. The ambient fluid is 20% polybutene in decane. Snapshots are taken 542 μs apart, the arrows indicate the capillary wave, and the horizontal lines indicate the top of the bubble in the first frame. (a) is the experimental result, reprinted with permission from Chen et al. (2006), Copyright 2006 American Institute of Physics. (b) is the simulation result. The figure is reprinted with permission from Ervik et al. (2014), Copyright 2013 Elsevier Inc.