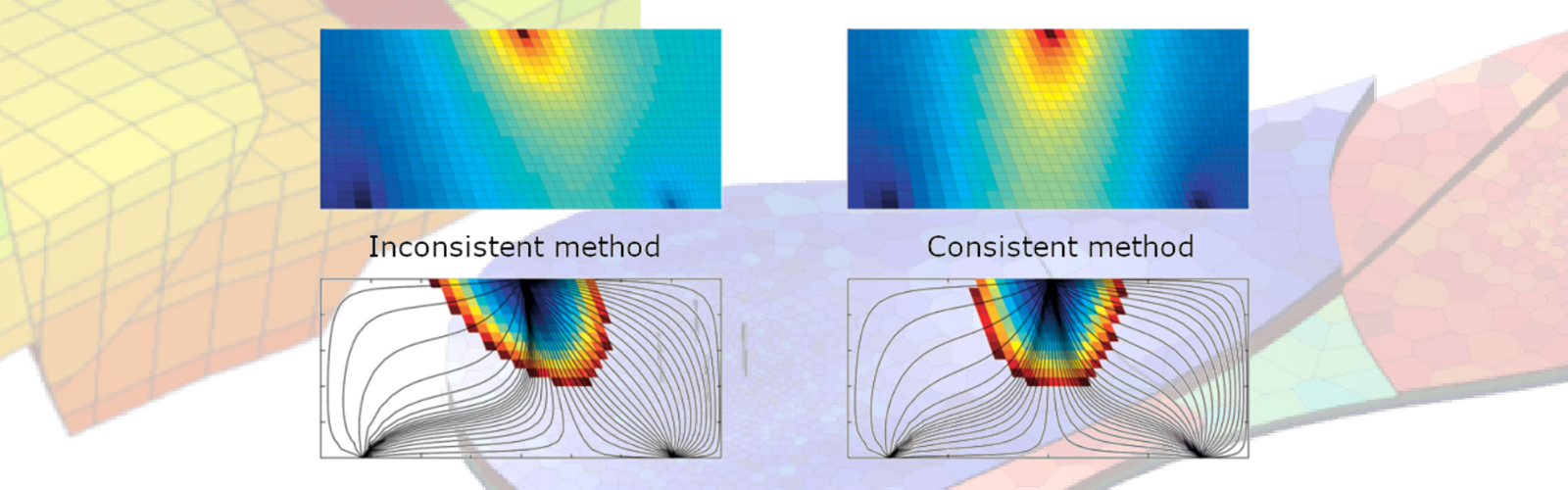
Grid-orientation errors resulting from inconsistent discretizations are particularly pronounced in simulating flow in porous media, where the conductivity tensor K usually is strongly anisotropic and complex polytopal grids are used to represent the intricate and heterogeneous nature of the media.
With extensive experience in analyzing inconsistency errors and implementing consistent schemes, we specialize in ensuring their efficacy on complex grids and for highly nonlinear flow models:
- Mixed hybrid finite element (MHFE) methods utilize both primal and dual variables to discretize partial differential equations, enabling efficient and accurate solutions for a wide range of problems.
- Mimetic finite difference (MFD) methods preserve key properties of continuous differential operators in their discrete counterparts, ensuring accurate and stable solutions for various physical problems.
- Virtual element methods (VEM) employ locally defined virtual elements to discretize partial differential equations on polygonal or polyhedral meshes, offering flexibility and accuracy for a wide range of applications.
- Multipoint flux approximation (MPFA) schemes accurately capture fluxes across control volumes by considering multiple neighboring grid points. Multipoint stress approximation (MPSA) schemes implement the same idea for mechanics.
- Nonlinear finite-volume (NFVM) methods rely on convex combinations of two linear consistent flux approximations, employing solution-dependent weights, to achieve monotonicity or preserve extremum principles that are not guaranteed in linear consistent methods.
- Vertex approximation gradient (VAG) methods use both nodal and cell-center degrees of freedom to ensure a consistent discretization; the latter are eliminated at the linear algebra level without fill-in.
All of these methods are available within our open-source MRST software suite.