|
MRST-core
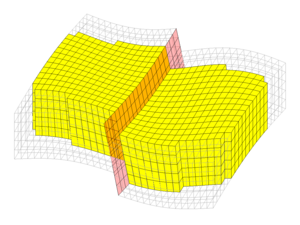
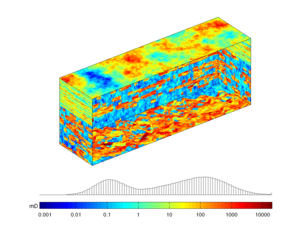
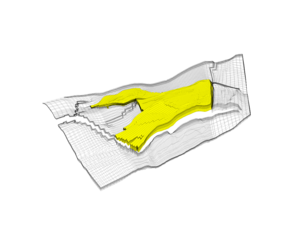
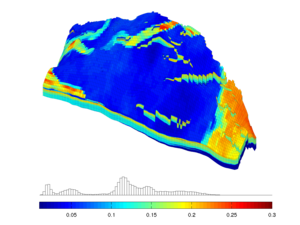
The core module contains routines and data structures for creating and manipulating grids, petrophysical data, and global drive mechanisms such as gravity, boundary conditions, source terms, and wells. The core also contains an implementation of automatic differentiation (you write the formulas and specify the independent variables,the software computes the corresponding derivatives or Jacobians) based on operator overloading, as well as a few routines for plotting cell and face data defined over a grid. The core module is designed to be as minimal as possible.
Literature
|
||||||||||||||||||||||||||||||||||||||