You are here:
MRST
/
Documentation
/
Tutorials
/
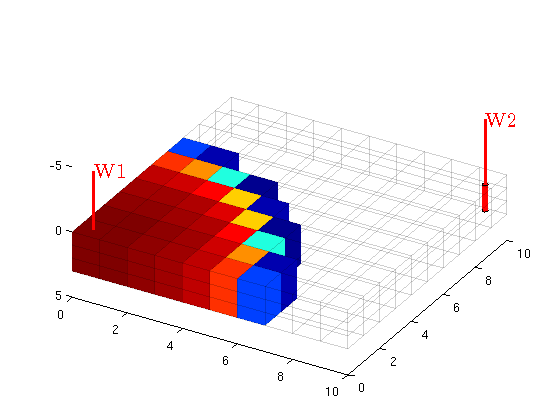
Visualization tutorial