Tutorials

Anisotropic permeability The example explains how to use the MPFA-O solver to solve a problem with homogeneous, anisotropic permeability. The resulting pressure solutions are compared and contrasted to similar solutions computed by the TPFA and a mimetic method.

Grid-orientation errors The MPFA-O scheme is consistent on grids that are not necessarily K-orthogonal. This example compares and contrasts grid-orientation effects for the MPFA-O, mimetic, and TPFA solvers for a single-phase flow problem with isotropic permeability represented on a curvilinear grid in which most cells are not K-orthogonal.

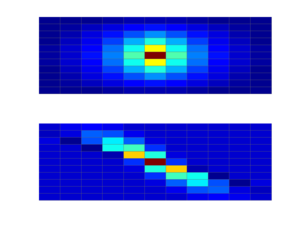
Description

To get a consistent discretization for anisotropic permeablities and general polyhedral grids, multipoint flux-approximation method use, as the name says, more than two points to approximate the flux across each inter-cell face. The mpfa module implements one such method, the MPFA-O method [1]. The implementation utilizes the fact that some variants of the method can be formulated as a mimetic method. In the resulting local-flux mimetic formulation [2,3] of the MPFA-O method, each face in the grid is subdivided into a set of subfaces, one subface per node that makes up the face. The inner product of the local-flux mimetic method gives exact result for linear flow and is block diagonal with respect to the faces corresponding to each node of the cell, but it is not symmetric. The block-diagonal property makes it possible to reduce the system into a cell-centered discretisation for the cell pressures. This naturally leads to a method for calculating the MPFA transmissibilities.

The module offers two basic routines

• incompMPFA - assembles and solves a system of linear equations to compute interface fluxes and cell and pressures based on multi-point flux approximation (MPFA) method with minimal memory consumption within the constraints of operating on a fully unstructured polyhedral grid structure
• computeMultiPointTrans - compute half-face transmissibilities using the MPFA-O method

The incompMPFA solver is compatible with the incompressible fluid models and transport solvers from the incomp module. 

See also: two-point and mimetic discretizations

Literature

1. I. Aavatsmark. An introduction to multipoint flux approximations for quadrilateral grids. Comput. Geosci., Vol. 6, No. 3, pp. 405–432, 2002. DOI: 10.1023/A:1021291114475
2. K. Lipnikov, M. Shashkov, and I. Yotov. Local flux mimetic finite difference methods. Numer. Math., Vol. 112, No. 1, pp. 115–152, 2009. DOI: 10.1007/s00211-008-0203-5
3. R.A. Klausen and A.F. Stephansen. Mimetic MPFA. ECMOR XI - 11th European Conference on the Mathematics of Oil Recovery. 2008. DOI: 10.3997/2214-4609.20146365
4. K.-A. Lie, S. Krogstad, I. S. Ligaarden, J. R. Natvig, H. M. Nilsen, and B. Skaflestad. Open source MATLAB implementation of consistent discretisations on complex grids. Comput. Geosci., Vol. 16, No. 2, pp. 297-322, 2012. DOI: 10.1007/s10596-011-9244-4