|
Incompressible Flow
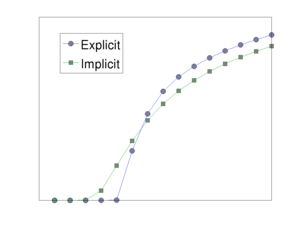
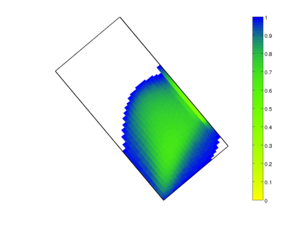
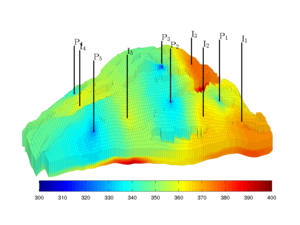
The module implements the basic fluid objects necessary to represent incompressible, two-phase flow. To solve these flow equations, the module offers a standard two-point flux-approximation (TPFA) method for pressure and explicit and implicit transport solvers using single-point upstream mobility weighting, which can be combined in sequential solution procedures.
Tutorials
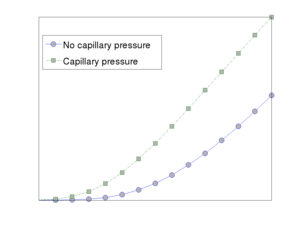
DescriptionMRST's fluid representation is a structure of function handles which compute fluid properties (e.g., density or viscosity), fluid phase saturations, and relative-permeability and capillary-pressure curves. This representation supports generic implementation of derived quantities such as mobilities or flux functions for a wide range of fluid models. The
To solve the resulting single-phase and two-phase incompressible fluid equations that can be modelled with the above fluid objects, the module offers three solvers:
The three solvers should, at least in principle, be applicable to any kind of incompressible fluid model that follows the same convention as the fluid objects already implemented in the module. It is therefore not difficult to extend the functionality of the module to contain other relative-permeability models, more phases, etc. The incomp module was originally implemented as part of MRST's core functionality, but has been moved to a separate module from release 2015a and onward. Literature
|
||||||||||||||||||||||||||||