Tutorials

	Example 1 The example explains how to use the mimetic pressure solver to solve the single-phase pressure equation for a flow driven by Dirichlet and Neumann boundary conditions.		Example 2 The example shows to use the mimetic framework to set up a solver that is identical to the classical TPFA solver on Cartesian grids, but unlike the TPFA method, is consistent also on grids that are not K-orthogonal.
	Example 3 This example considers a quarter five-spot problem with wells controlled by either pressure or by rate. Solutions are computed with the TPFA method and by the mimetic method with a two-point inner product.		Example 4 One approach to modelling conduits and barriers to flow is to introduce scalar multipliers on the two-point transmissiblity of a set of grid block connections (cell interfaces). The example shows how to incorporate such multipliers in a mimetic discretization.

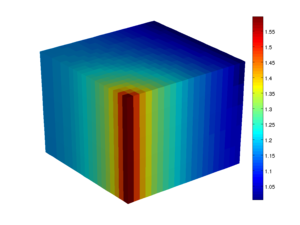
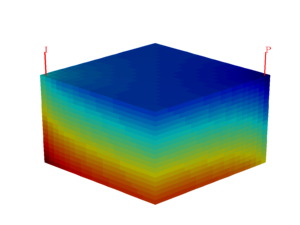
Description

The standard two-point flux approximation method implemented in the incomp module is not consistent and hence not convergent unless the grid is K-orthogonal. The incompTPFA solver may therefore give significant grid-orientation errors for anisotropic permeabilities and skew grids.

This module implements a family of first-order mimetic methods that give consistent discretizations of Poisson-type flow equations on general polyhedral and polygonal grids. The mimetic method is an example of a so-called compatible spatial discretizations, which are designed so that they not only provide accurate approximation of the flow equation but also inherit or mimic fundamental properties of the underlying differential operators. The mimetic method is constructed by requiring that the discretization correctly reproduces a linear pressure drop on general grids. This introduces certain freedom, and by carefully picking the parameters that are needed to fully specify a method, one can construct mimetic methods that coincide with other known methods, or reduce to these methods (e.g., the two-point method, the Raviart--Thomas mixed finite-element method, or the MPFA-O multipoint method) on certain types of grids.

The module offers two basic routines

• incompMimetic - assembles and solves a (block) system of linear equations defining interface fluxes and cell and interface pressures
• computeMimeticIP - compute the mimetic inner product that determines which type of scheme the mimetic method should reduce to on simple grids

The incompMimetic solver is compatible with the incompressible fluid models and transport solvers from the incomp module. It can assemble and solve the flow equations in three different ways:

1. Assemble and solve hybrid system for interface pressures. The system is eventually solved by Schur complement reduction and back substitution. This is the default behavior of the solver.
2. Assemble and solve a hybrid system for interface pressures, cell pressures and interface fluxes. The system is eventually reduced to a mixed system.
3. Assemble and solve a cell-centred system for cell pressures. Interface fluxes recovered through back substitution.

MRST was originally developed to support research on consistent discretizations on general polyhedral grids. The mimetic solver was therefore tightly interwoven with the rest of the functionality in early versions of the software. More recently, the mimetic part has been separated from the fluid objects specifying incompressible flow models and moved to a separate module.

See also: two-point discretization and MPFA 

Literature

1. K.-A. Lie. An Introduction to Reservoir Simulation Using MATLAB/GNU Octave: User guide for the MATLAB Reservoir Simulation Toolbox (MRST). Cambridge University Press, to appear.
2. K.-A. Lie, S. Krogstad, I. S. Ligaarden, J. R. Natvig, H. M. Nilsen, and B. Skaflestad. Open source MATLAB implementation of consistent discretisations on complex grids. Comput. Geosci., Vol. 16, No. 2, pp. 297-322, 2012. DOI: 10.1007/s10596-011-9244-4