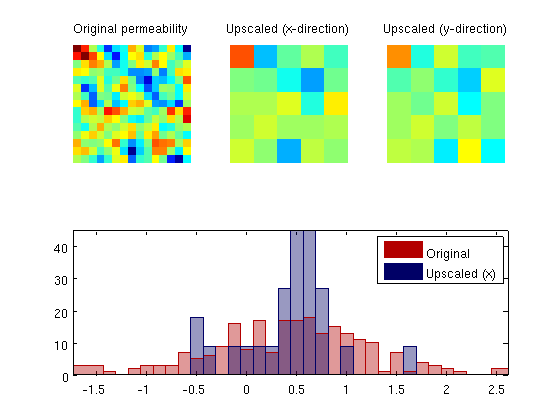
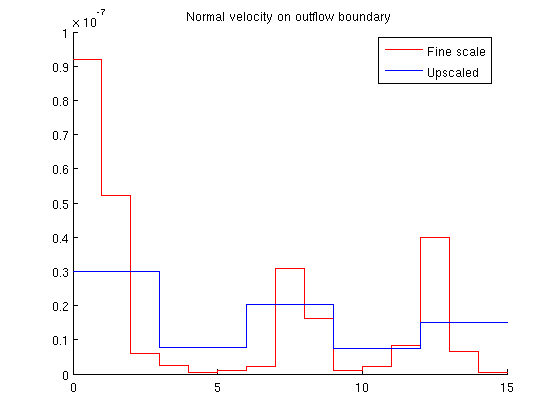
You are here:
MRST
/
Modules
/
Upscaling
/
Single-Phase Upscaling