MRSTlogo_web_banner_light_thinner_Epi.png

Multiscale Mixed Finite Elements Module
The basic idea of the MsMFE method is to use a mixed finite-element method on a coarse scale with special basis functions that satisfy local flow problems and thereby account for subgrid variations. This way, an approximate fine-scale solution is constructed at the cost of solving a coarse-scale problem

Tutorials

MsMFE on Cartesian grids

We discuss the MsMFE method for solving the single-phase pressure equation on a Cartesian grid with isotropic, homogeneous permeability 
Read more...		  

MsMFE on corner-point grids

We demonstrate how to use the multiscale flow solver for a simple corner-point model with wavy geometry and a single fault.
Read more ...

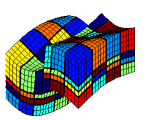
Description

The MsMFE method is formulated using two grids, a fine underlying grid on which the media properties are given, and a coarse simulation grid where each block can consists of an arbitrary connected collection of cells from the fine grid. In this sense, the method is very flexible and can be applied to almost any grid, structured or unstructured, and can easily be built on-top-of existing pressure solvers.

The MsMFE offers fast, accurate, and robust pressure solvers for highly heterogeneous porous media and can be used for

  • direct simulation on high-resolution grid models with multimillion cells
  • fast simulation of multiple (stochastic) realisations of reservoir heterogeneity
  • model reduction to provide instant simulation of flow responses

Read more...

Literature

The basics of the method is described in the following papers:

  1. J. E. Aarnes, S. Krogstad, and K.-A. Lie. Multiscale mixed/mimetic methods on corner-point grids. Computational Geosciences, Special issue on multiscale methods, 2008. DOI: 10.1007/s10596-007-9072-8
  2. J. E. Aarnes, S. Krogstad, and K.-A. Lie. A hierarchical multiscale method for two-phase flow based upon mixed finite elements and nonuniform coarse grids, Multiscale Modelling and Simulation, Vol. 5, No. 2, pp. 337-363, 2006. DOI: 10.1137/050634566.

In addition, we list a few selected papers that show applications of the MsMFE method:

  1. M. Pal, S. Lamine, K.-A. Lie, and S. Krogstad Multiscale method for simulating two and three-phase flow in porous media. Paper SPE 163669 presented at the 2013 SPE Reservoir Simulation Symposium, The Woodlands, Texas, USA, 18-20 February 2013.
  2. J. R. Natvig, K.-A. Lie, S. Krogstad, Y. Yang, and X.-H. Wu. Grid adaption for upscaling and multiscale methods. Proceedings of ECMOR XIII, Biarritz, France, 10-13 September 2012.
  3. F. O. Alpak, M. Pal, and K.-A. Lie. A multiscale method for modeling flow in stratigraphically complex reservoirs. SPE J., Vol. 17, No. 4, pp. 1056-1070, 2012. DOI: 10.2118/140403-PA
  4. S. Krogstad, K.-A. Lie, and B. Skaflestad. Mixed multiscale methods for compressible flow. Proceedings of ECMOR XIII, Biarritz, France, 10-13 September 2012.
  5. J. R. Natvig, B. Skaflestad, F. Bratvedt, K. Bratvedt, K.-A. Lie, V. Laptev, and S. K. Khataniar. Multiscale mimetic solvers for efficient streamline simulation of fractured reservoirs. SPE J., Vol. 16, No. 4, pp. 880-880, 2011. DOI: 10.2018/119132-PA
  6. S. Krogstad, K.-A. Lie, H. M. Nilsen, J. R. Natvig, B. Skaflestad, and J.E. Aarnes. A multiscale mixed finite-element solver for three-phase black-oil flow. Paper SPE 118993 presented at the 2009 SPE Reservoir Simulation Symposium, The Woodlands, Texas, USA, 2-4 February.
  7. A. F. Gulbransen, V. L. Hauge, and K.-A. Lie. A multiscale mixed finite-element method for vuggy and naturally-fractured reservoirs. SPE J., Vol. 15, No. 12, pp. 395-403, 2010. DOI: 10.2118/119104-PA

Download

This module is bundled with MRST Core in the standard release.

Published October 1, 2012