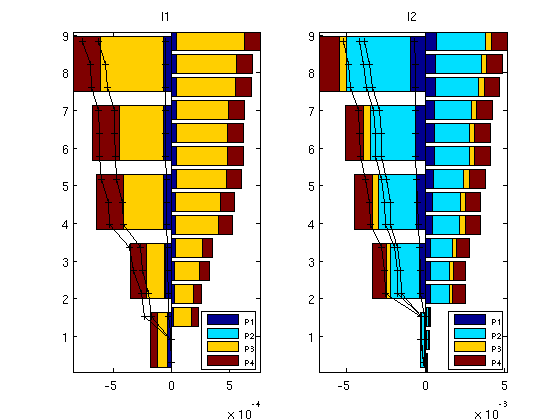
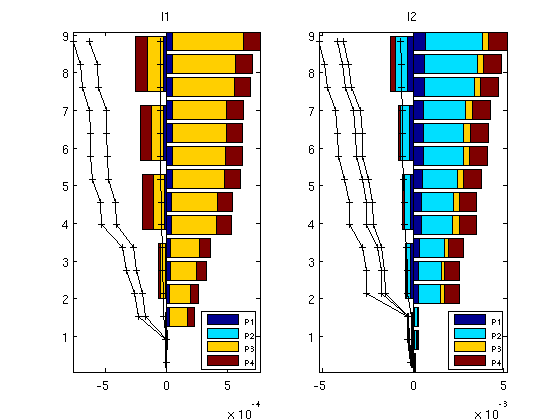
You are here:
MRST
/
Modules
/
Flow diagnostics
/
Validating upscaling methods