You are here:
MRST
/
Modules
/
Flow diagnostics
/
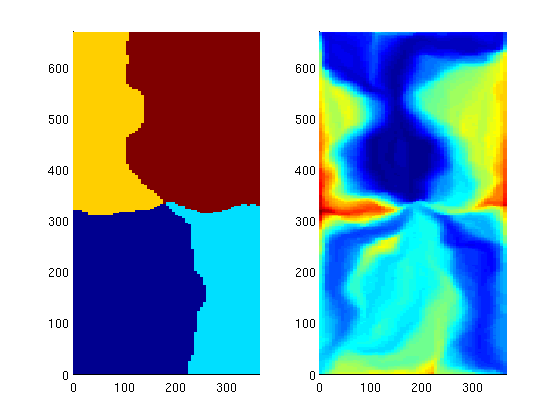
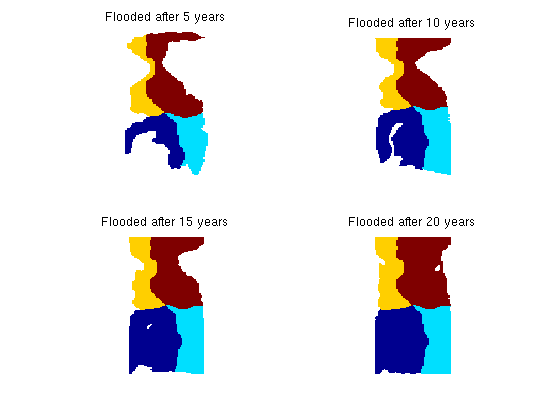
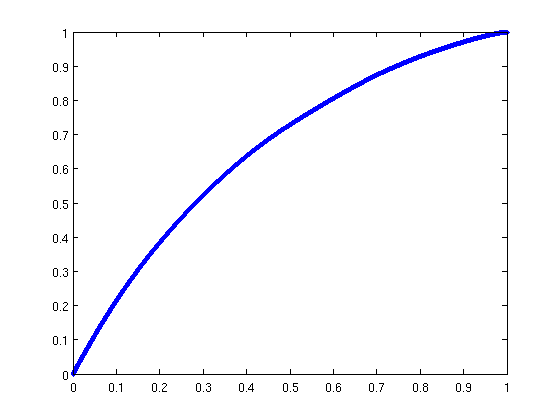
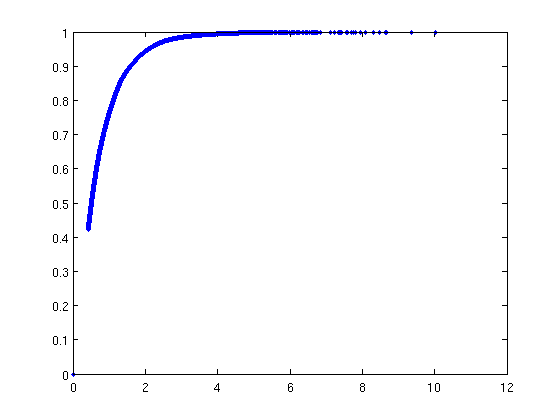
Basic flow diagnostics