Sleipner is a comercial CO₂ storage site in the North Sea, where CO₂ has been injected since 1996.

In this example we simulate injection and migration of CO₂ on sleipner using the data provided in the paper:

   "Reservoir Modeling of CO2 Plume Behavior Calibrated Agains
   Monitoring Data From Sleipner, Norway", SPE 134891

The data set is avaliable online on: http://www.ieaghg.org/index.php?/2009112025/modelling-network.html

Provided with the paper is injection rates for 11 years. We inject 30 years using the last injection rate the last 19 years.

We demonstrate the use of C/C++-accelerated MATLAB, using the functions

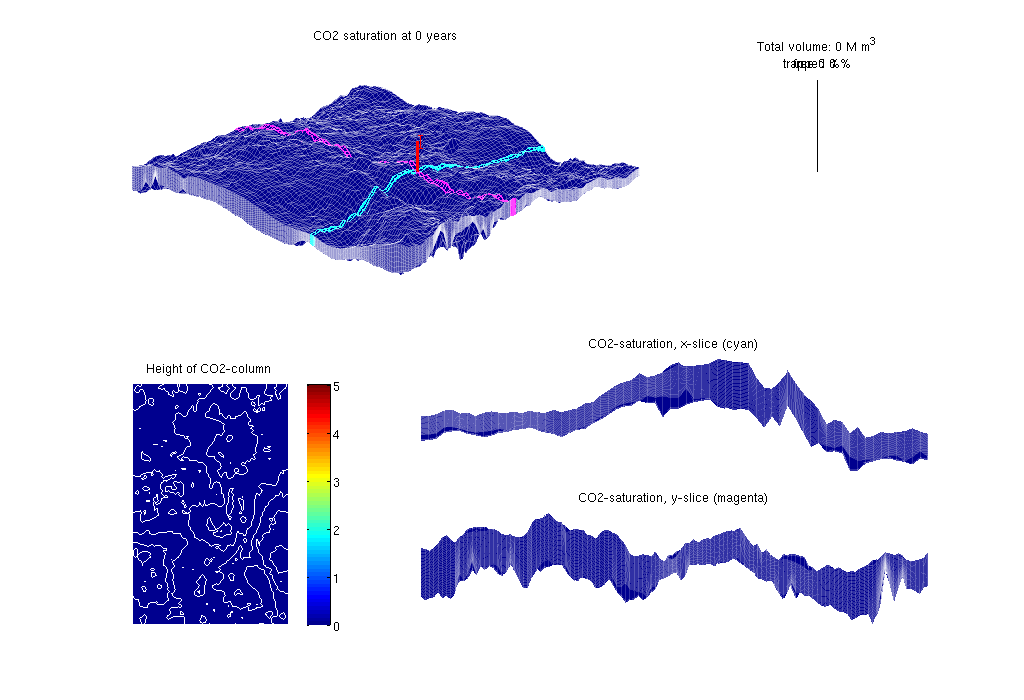
The last mentioned function requires that you have built the solver in the src/VEmex directory.

Contents

Display header

clc
disp('================================================================');
disp('   Vertical averaging applied to the Sleipner model');
disp('   using C++ accelleration in the transport solver');
disp('================================================================');
disp(' ');

================================================================
   Vertical averaging applied to the Sleipner model
   using C++ accelleration in the transport solver
================================================================
 

Construct stratigraphic, petrophysical, and VE models

The 3D model consists of a grid (G) and petrophysical parameters (rock). The VE model consists of a top-surface grid (Gt), petrophysical data (rock2D), and indices to the boundarcy cells where we will supply pressure boundary conditions. Called with a true flag, the routine will use C-accelerated MATLAB routines to process the data input and compute geometry. Once the models are created, they are stored in a data file for faster access at a later time.

[G, Gt, rock, rock2D, bcIxVE] = makeSleipnerVEmodel(true);

 -> Reading Sleipner.mat

Set time and fluid parameters

Fluid data are taken from paper SPE 134891

gravity on
T          = 250*year();
stopInject = 30*year();
dT         = 1*year();
dTplot     = dT;
fluidVE    = initVEFluidHForm(Gt, 'mu' , [6e-2*milli 8e-4]*Pascal*second, ...
                         'rho', [760 1200] .* kilogram/meter^3, ...
                         'sr', 0.21, 'sw', 0.11, 'kwm', [0.75 0.54]);

Set well and boundary conditions

The well is placed near the actual injection site. The injection rates are taken from the beforementioned paper. Hydrostatic boundary conditions are specified on all outer boundaries.

disp(' -> Setting well and boundary conditions');

% Set well in 3D model
wellIx = [36 78 7];
rates  = [2.91e4; 5.92e4; 6.35e4; 8.0e4; 1.09e5; ...
         1.5e5; 2.03e5; 2.69e5; 3.47e05; 4.37e5; 5.4e5]*meter^3/year;
W      = verticalWell([], G, rock, wellIx(1), wellIx(2), ...
                      wellIx(3), 'Type', 'rate', 'Val', rates(1), ...
                      'Radius', 0.1, 'comp_i', [1,0], 'name', 'I');

% Well in 2D model
WVE = convertwellsVE(W, G, Gt, rock2D);

% BC in 2D model
bcVE = addBC([], bcIxVE, 'pressure', ...
            Gt.faces.z(bcIxVE)*fluidVE.rho(2)*norm(gravity));
bcVE = rmfield(bcVE,'sat');
bcVE.h = zeros(size(bcVE.face));

 -> Setting well and boundary conditions

Prepare simulations

Compute inner products and instantiate solution structure

disp(' -> Initialising solvers');
SVE = computeMimeticIPVE(Gt, rock2D, 'Innerproduct','ip_simple');
preComp = initTransportVE(Gt, rock2D);
sol = initResSolVE(Gt, 0, 0);
sol.wellSol = initWellSol(W, 300*barsa());
sol.s = height2Sat(sol, Gt, fluidVE);

% Find trapping structure in grid. Used for calculation of trapped volumes
ts=findTrappingStructure(Gt);

% Select transport solver
% Use C++ acceleration if it exists - NB: requires the VEmex module
% Notice that the two solvers determine the time steps differently and
% may therefore give slightly different answers.
try
   mtransportVE;
   cpp_accel = true;
catch me
   disp('mex-file for C++ acceleration not found');
   disp(['See ', fullfile(VEROOTDIR,'VEmex','README'), ' for building instructions']);
   disp('Using matlab VE-transport');
   cpp_accel = false;
end

 -> Initialising solvers
Trap level 1: 197 traps identified
Trap level 2: 34 traps identified
Trap level 3: 2 traps identified
Trap level 4: 1 traps identified

Prepare plotting

We will make a composite plot that consists of several parts: a 3D plot of the plume, a pie chart of trapped versus free volume, a plane view of the plume from above, and two cross-sections in the x/y directions through the well

opts = {'slice', wellIx, 'Saxis', [0 1-fluidVE.sw], ...
   'maxH', 5, 'Wadd', 10, 'view', [130 50]};
plotPanelVE(G, Gt, W, sol, 0.0, [0 0 1], opts{:});

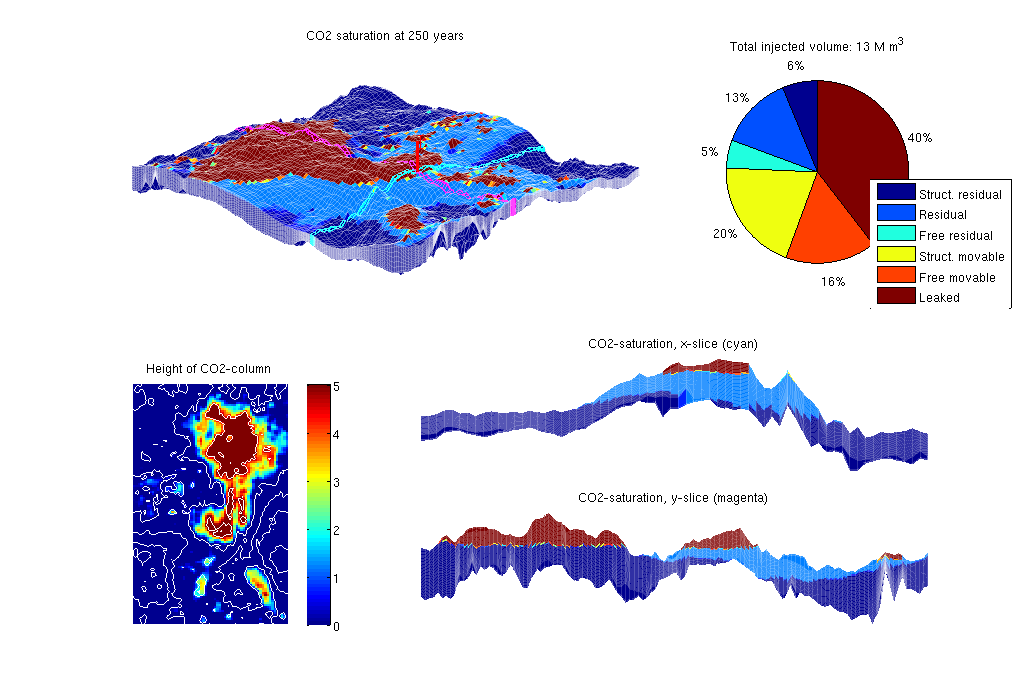
Main loop

Run the simulation using a sequential splitting with pressure and transport computed in separate steps. The transport solver is formulated with the height of the CO₂ plume as the primary unknown and the relative height (or saturation) must therefore be reconstructed.

t = 0;
totVol = 0.0;
fprintf(1,'\nSimulating %d years of injection', convertTo(stopInject,year));
fprintf(1,' and %d years of migration\n', convertTo(T-stopInject,year));
fprintf(1,'Time: %4d years', convertTo(t,year));

w = WVE;
tic
while t<T
   % Advance solution: compute pressure and then transport
   sol = solveIncompFlowVE(sol, Gt, SVE, rock, fluidVE, ...
      'bc', bcVE, 'wells', w);

   if cpp_accel
      [sol.h, sol.h_max] = mtransportVE(sol, Gt, dT, rock, ...
                                          fluidVE, 'bc', bcVE, 'wells', w, ...
                                          'gravity', norm(gravity));
   else
      sol = explicitTransportVE(sol, Gt, dT, rock, fluidVE, ...
                               'bc', bcVE, 'wells', w, 'preComp', preComp, ...
                               'intVert', false);
   end

   % Reconstruct 'saturation' defined as s=h/H, where h is the height of
   % the CO2 plume and H is the total height of the formation
   sol.s = height2Sat(sol, Gt, fluidVE);
   assert( max(sol.s(:,1))<1+eps && min(sol.s(:,1))>-eps );
   t = t + dT;

   % Add the volume injected during last time step to the total volume
   % and compute trapped and free volumes
   if ~isempty(w)
      totVol = totVol + w.val*dT;
   end
   vol = volumesVE(Gt, sol, rock2D, fluidVE, ts);

   % Check if we are to stop injecting or change injection rate
   if t>= stopInject
      w  = []; dT = 5*year(); dTplot = dT;
   else
      ind = min(floor(t/year)+1, numel(rates));
      rate = rates(ind);
      w.val = rate;
   end

   % Plotting
   fprintf(1,'\b\b\b\b\b\b\b\b\b\b%4d years', convertTo(t,year));
   if mod(t,dTplot)~= 0 && t<T,
      continue
   else
      plotPanelVE(G, Gt, W, sol, t, [vol totVol], opts{:});
      drawnow
   end
end
fprintf(1,'\n\n');
% delete C++ simulator
if cpp_accel, mtransportVE; end
etime = toc;
disp(['Elapsed simulation time: ', num2str(etime), ' seconds.']);

Simulating 30 years of injection and 220 years of migration
Time:  250 years

Elapsed simulation time: 242.3689 seconds.

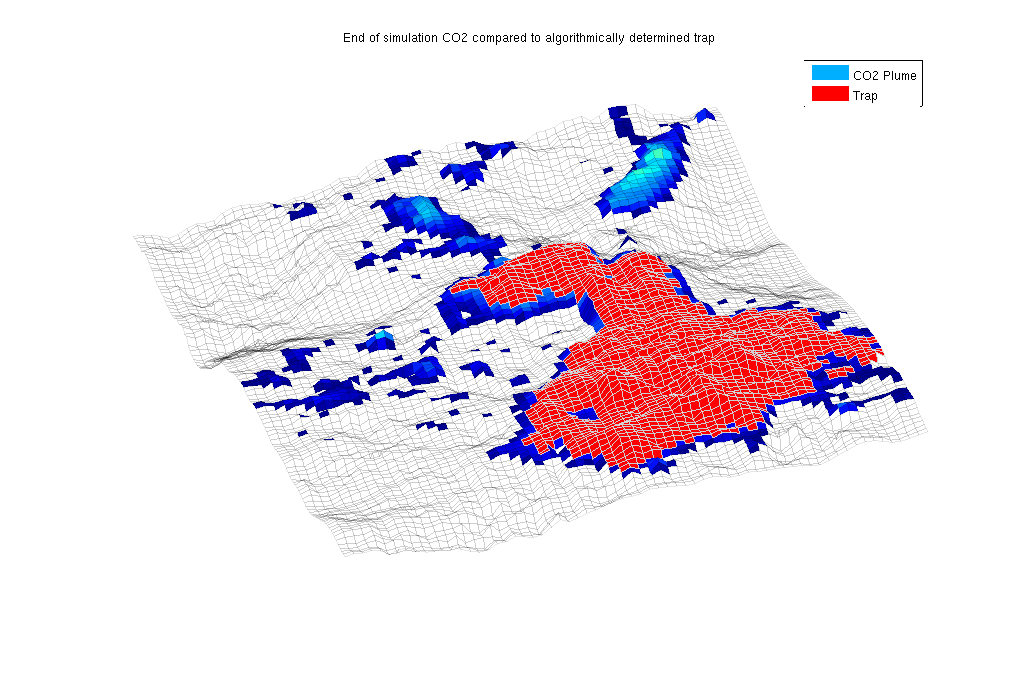
Show the structural trap

After the simulation has completed, we are interested in seeing how the location of the CO₂ plume after a long migration time corresponds to the trapping estimates produced by trapAnalysis. This is done by finding the trap index of the well injection cell and then plotting the trap along with the final CO₂ plume.

% Generate traps and find the trap corresponding to the well cells
res = trapAnalysis(Gt, false);
trap = res.trap_regions([WVE.cells]);

% Plot the areas with any significant CO2 height along with the trap in red
clf;
plotCellData(Gt, sol.h, sol.h > 0.01)
plotGrid(Gt, res.traps == trap, 'FaceColor', 'red', 'EdgeColor', 'w')
plotGrid(Gt, 'FaceColor', 'None', 'EdgeAlpha', .1)

legend({'CO2 Plume', 'Trap'})
axis tight off
view(-20, 75)
title('End of simulation CO2 compared to algorithmically determined trap')