2024: Graphs and Applications

The 24th Geilo Winter School took a dive into the world of graphs and their applications, covering topics from how to best model graphs in Python to spectral theory to graph neural networks. 

2023: Computational Statistics

The 23rd Geilo Winter School covered the topic of computational statistics, which is of great importance in a number of modern applications. The lectures ranged from introductions to Monte Carlo methods, MCMC and friends, Bayesian inference and Integrated Nested Laplace Approximation to using Julia for computational statistics and even covered some reinforcement learning.

2022: Continuous Optimization

Continuous optimization is the study of maximizing functions of continuous variables. Such problems are generally intractable without additional conditions and constraints, but for many specific cases, theoretical research has led to the development of very useful algorithms for practical applications. Today, such algorithms constitute the workhorse in a diverse range of applications spanning from robotics over machine learning to economics. Recent successes in the field include progress in compressed sensing and advances in large-scale optimization.

In the school of 2022 we looked into a number of exciting topics ranging from continuous optimization basics to topics like shape optimization, PDE-constrained optimization, and the relationship between machine learning and optimization. 

2021: Explainable Algorithms

The past decade has seen impressive developments in powerful machine learning algorithms. These methods have been most successful when applied to problems where other tools are not readily available, and today frequently guide many decision-making processes. Much recent research focuses on applying these methods in areas where machine learning and statistical methods are not commonly part of the toolbox in order to tackle parts of the problem that are hard to solve by traditional approaches. In these cases, a proper understanding of what the algorithms are in fact telling us is very important. An example is in numerical simulation, where machine learning can be used for parameter estimation, acceleration of linear and nonlinear solvers, or even as proxy models where the governing equations merely serve as physical constraints. On the other hand, numerical tools can also be used to enhance our understanding of applied machine learning algorithms.

In the 2021 winter school, we took a deep dive into explainable algorithms, and aimed to understand how an algorithm can be efficient, robust and comprehensible at the same time.

2020: Modern Techniques and Algorithms in High-Performance Computing

Modern multicore and parallel CPU and GPU architectures have made it possible to handle problems that were far out of reach not so long ago. Moreover, there is an increasing interest in quantum computers, which have the potential of opening entirely new avenues of algorithmic research. Exploiting the numerical potential of modern computing platforms requires knowledge and training in high-performance computing (HPC). This winter school looked at important topics related to HPC, including:

• GPU computing
• Quantum computing
• Automatic differentiation
• Distributed parallelism

2019: Learning from Data

The availability of ever more computing power and data has led to an enormous development in methods related to data in the recent years. In this winter school, we will look at methods for using the knowledge in data to improve our computer algorithms and look at the interplay between these. The school will focus around the following topics and try to connect the dots between these interrelated fields:

• Data assimilation
• Inverse modeling and parameter estimation
• Uncertainty quantification
• Value of information
• Machine learning and artificial intelligence

2018: Practical artificial intelligence

The 2018 edition was an exciting new school on the topic of Practical use of Artificial Intelligence. Techniques within artificial intelligence are now able to extract knowledge from vast amounts of data on level we have not seen before, and AI has been a game changer for a range of application areas in recent years. This winter school will focus on the practical aspects of artificial intelligence and equip participants with the skills required to run machine learning tasks on their own data targeting their problems. Part of the school will be a tutorial on using artificial intelligence techniques, with a large number of hands-on exercises for participants to fully grasp the topic. The aim is that the school becomes an interactive workshop with a high level of participant involvement. During the course of the winter school, you will learn different techniques, which libraries that implement these, and try them out for yourself. Participants are encouraged to prepare their own data and problems that they want to solve during the winter school.

2017: Machine Learning, Deep Learning, and Data Analytics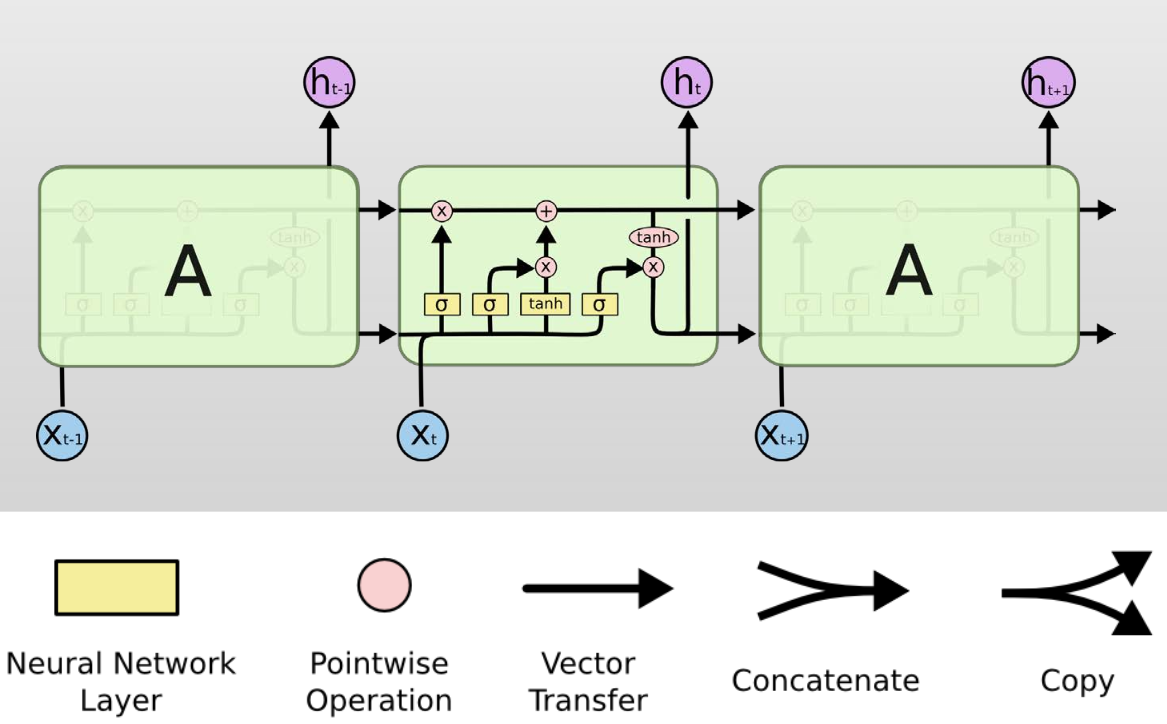

The 2017 winter school topic will be machine learning, deep learning, and data analytics. The digitalization wave has brought with it an explosion in the variety and number of data sources, ranging from various physical sensors to text, video, audio, social networks, and simulation results. Traditional techniques such as simple statistics has shown to be insufficinent with such complex and massive data, but developments within artificial intelligence and machine learning has in the recent years shown great promise. Techniques within artificial neural networks, deep learning and data analytics are now able to extract knowledge hidden in vast amounts of data in a way on a level we have not seen before. Algorithms within artificial intelligence are often applicable to a wide range of application areas, and the aim of this winter school is that participants should learn concepts, techniques, and algorithms for use in their own research.

2016: Scientific Visualization

Visualization is an integral part of science, and a necessity for our understanding of complex processes and data. The word visualization can have a broad interpretation, including creating trivial plots of values, advanced rendering techniques, and complex statistical data reasoning. This winter school will target the process of understanding data through scientific visualization, and focus on extracting knowledge from data. With hands-on exercises you will during the course of this winter school learn techniques, tools, and best practices for extracting knowledge from data.

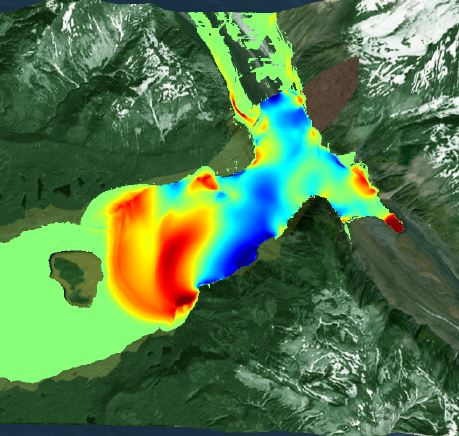2015: Uncertainty Quantification for Physical Phenomena

This year's winter school covers the topic of uncertainty quantification for simulation of physical phenomena. Uncertainty quantification aims to answer the questions "How accurate are the results?", and "Where are the largest uncertainties?", and the winter school will cover both intrusive and non-intrusive methods. We will learn from experts in the field on topics including multi-level Monte Carlo and ensemble simulations, polynomial chaos, and inverse problems.

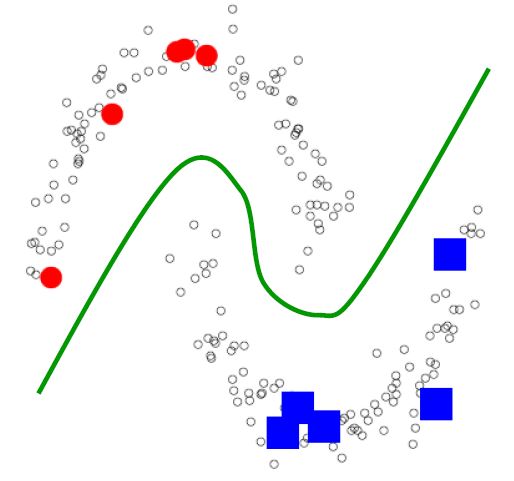2014: Big Data Challenges to Modern Statistics

Traditional statistical methodology is challenged by more and more complex and high-dimensional data and subtile scientific questions. This winter school will give you a panoramic overview and selective in-depth details, of some of the most important innovative statistical theories, methods and computational tools that are being developed. You will be introduced to: challenging statistical problems that require intensive computational approaches, structural model learning, causal inference, graphical models, functional data analysis, tree structured data, spatial data, point patterns and shape analysis, and more, both in a frequentist and bayesian perspective. Applications will span from genomics to computational anatomy, from ice with air bubbles images to geology, from human movement recognition to neurobiology, from networks to personalise therapy.

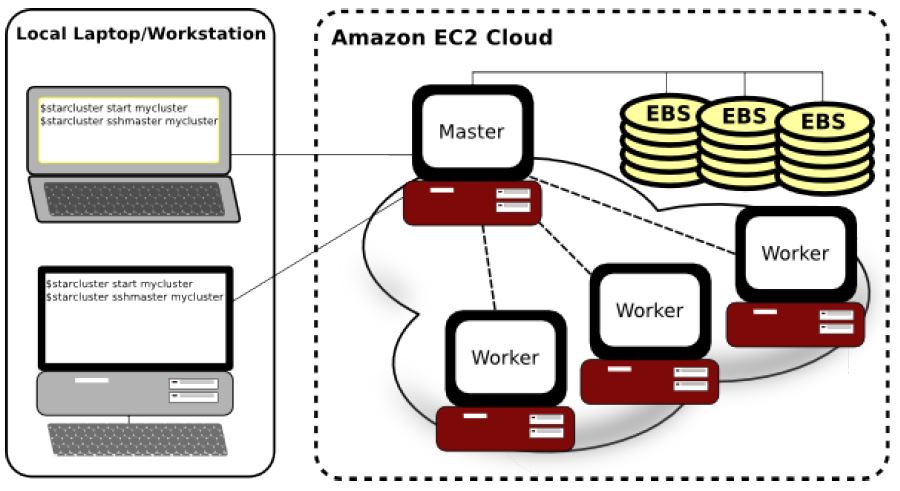2013: Reproducible Science And Modern Scientific Software

A major problem with the computational science community today is that many publications are impossible to reproduce. Results published in a paper are seldom accompanied by the source code used to produce these results. Even when the source code is available the published results can only be reproduced if run the code is compiled with a specific compiler and run on a specific architecture using a specific set of parameters. Reproducibility aims to make the process of publishing reproducible science as simple as possible, and it has gained a lot of momentum as a desirable principle of the scientific method. Tightly coupled with reproducible science is modern software development. Tools and methodologies including version control, unit testing, verification and validation, and continuous integration make the process of publishing reproducible science much simpler.

2012: Introduction to Continuum Mechanics

The 2012 winter schoolwill give an introduction to the use of continuum mechanics for mathematically modeling physical phenomena: from identifying the governing equations of the physics, to the numerical discretization and simulation. Many graduate students and young researchers within eScience have a good background in mathematics, statistics, and computer science but lack important information about how the models they study arise. This year's winter school will give a lecture series on computational modeling with emphasis ofn continuum mechanics, within industrial and biomedical problems.

2011: Mathematical and numerical methods for multiscale problems

Almost all problems in science and engineering involve processes and mechanisms that act on multiple spatial and temporal scales. Physical and man-made systems can be described on many levels, from quantum mechanics and molecular dynamics, via the mesoscale or nano-level, to continuum and system-level descriptions. For a specific problem, it is common to refer to the particular scale one is interested in as the macroscale. Scales smaller than the macroscale are often referred to as microscale, and sometimes one also introduces intermediate scales that are referred to as mesoscales. A multiscale problem can be defined as a problem where the macroscopic behaviour of a system is strongly affected by processes and properties from micro- and mesoscales. Solving the 'whole' problem at once is seldom possible as it would involve too many variables or too large scale differences to be computationally tractable, even on today's largest supercomputers. The traditional alternative has therefore been to compute effective parameters and usethese to communicate information between models on different scales. However, as the need for more accurate modelling increases, traditional homogenization and upscaling methods are becoming inadequate to answer advanced queries about multiscale problems. In some cases, effective properties may not be suffcient to properly describe complex interactions between macroscale and microscale processes; in other cases, one may not even know what are the correct properties to average.

2010: Automatic Differentiation

Automatic differentiation (or algorithmic differentiation) is a method for automatically augmenting a computer program with statements that computes the numerical derivatives of a function specified by the program. Any function, no matter how complex, can be decomposed into a sequence of elementary operation, each of which can be differentiated by a simple table lookup. By applying the chain rule repeatedly to these elementary operations, one can automatically compute derivatives of arbitrary order (such as gradients, tangents, Jacobians, Hessians, etc) that are accurate to working precision. Automatic differentiation is an alternative to symbolic and numerical differentiation.

2009: Optimization

Probably all of us, in private and work situations, try to find the best possible solution to problems. I could for example be searching for the best wines for a gourmet dinner, looking for the quickest way home, finding the least costly stock investment, or even trying to find the best design for an airplane wing. In Latin, optimum is a conjugation of optimus, which in turn is a superlative for bonus, which means good. Optimization is about finding the best solution, given certain prerequisites or constraints. In statistics, chemistry, biology, finance, geometry, operations research, and many other areas we come across problems classified as optimization problems. Often, optimization is the better half of simulation. Even though optimization problems differ; they all share the objective of either minimizing or maximizing a function under given constraints. Dependent on the specific objective function being optimized and the given constraints, you have different problem types that differ both in hardness and when it comes to suitable solution methods.

2008: Parallel Computing

For many decades the speed of computers has doubled every 1.5-2 years, which has meant that a program runs 50-100 times faster ten years after it was first written, without any change to the code itself. This is not likely to be the case in the future. Today, the main source of increased speed is that computers are gaining more processors so that they can perform several operations in parallel. In addition, specialised resources like graphics cards which are available in all computers are increasingly being exploited for general purpose scientific computations. To make full use of these resources you must change your code and perhaps even change your algorithm. So while parallel computing in the past has been of interest only to those who need to utilise the most powerful computers, parallel techniques are now becoming essential for anybody who wishes to fully make use of their desktop or laptop computer. This development also brings with it new approaches to parallel computing and it is not at all clear that the classical supercomputing approach is the best way to exploit the resources in your laptop.

2007: Monte Carlo Methods

The 2007 winter school in eScience is organized the week January 28 to February 2 at Dr. Holms Hotel, Geilo, Norway. Through the winter schools (four planned in the years 2007-2010) we wish to develop a supplementary forum for dissemination of modern theory and methods in mathematics, statistics and computer science. The winter schools will be given on a national basis, and will therefore contribute to a broader contact between students at the different universities and researchers in the institutes and the industry. The winter schools are also open to participants from outside Norway.

2006: Finite Element Method and Turbulent Flow Simulation

In the first part of this winter school, Hoffman and Logg will give an introduction to the techniques behind the FEniCS project. The vision of FEniCS is to set a new standard computational mathematics with respect to generality, efficiency, and simplicity concerning mathematical methodology, implementation, and application. In the second part, Hoffman will introduce a nonstandard approach to turbulence modelling based upon adaptivity and discretization by stabilized Galerkin finite element methods.

2005: Inverse Problems and Parameter Identification for PDE models

The topic of the fifth winter school is inverse problems and parameter identification for PDE models. The winter school lasts one week from Sunday to Friday before lunch and consists of 16 double lectures. The lecturers include topics on linear inverse problems, parameter identification problems for PDEs, parameter identification by level set and related methods, and inverse problems arising in connection with ECG (electrocardiogram) recordings

2004: Adaptive Methods for PDEs with Emphasis on Evolutionary Equations

The topic of the fourth winter school is adaptive methods for PDEs with particular emphasis on evolutionary equations. Lecturers are Mats G. Larson (Chalmers) and Rolf Rannacher (Heidelberg). The winter school lasts one week from Sunday to Friday evening and consists of approximately 15 double lectures. The lectures will give a self-contained presentation of adaptivity, starting with an introduction to simple principles and ending with advanced applications and recent results. We assume no specialized knowledge of adaptive methods, but the attendants are assumed to have general knowledge of numerical methods for partial differential equations.

2003: Modern Numerical Methods for Nonlinear Partial Differential Equations and Level Set Technology

The third winter school will cover two topics: modern numerical methods for nonlinear partial differential equations and level set technology for front propagation problems with applications to CFD and image processing. We will assume no specialized knowledge in the topics, but the attendants are assumed to have general knowledge of numerical methods for partial differential equations. Kenneth Hvistendahl Karlsen (UiB) and Helge Holden (NTNU) are responsible for the scientific contents of the lectures.

2002: Modern Computational Methods for Fluid Dynamics

The topic of the second winter school is modern computational methods for fluid dynamics. Kenneth Hvistendahl Karlsen (UiB) and Helge Holden (NTNU) were responsible for the scientific contents of the lectures. The emphasis will be on developing discretization and solution algorithms for solving the unsteady, incompressible Navier-Stokes equations. The applications will be selected from the laminar to the transitional flow regime.

2001: Parallel Computing with Emphasis on Clusters

The topic of the first winter school is parallel computing with special emphasis on Linux or Beowulf clusters. The winter schools are held at Norwegian ski resorts and there will be time in the program for skiing and for other social activities in the evenings. The winter schools should therefore provide a perfect arena for making new contacts with other researchers.