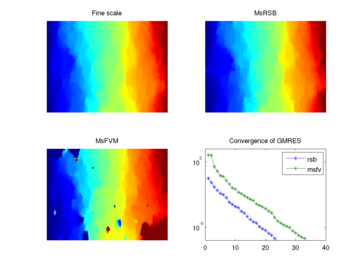
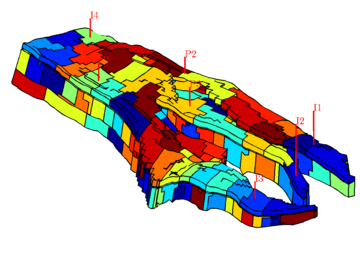
|
Chapter proposal for a forthcoming book on MRST
All prospective authors of a chapter in the new MRST book must express their interest to the editors as soon as possible, and in any case, no later than September 15 2019. The expression of interest does not need to follow any specific format, but must contain the information described below. For illustration, we have filled in content for a plausible chapter contribution.
Please send this information to the editors with the subject line "Chapter proposal for MRST book", and |
||||||||||||||||||||||