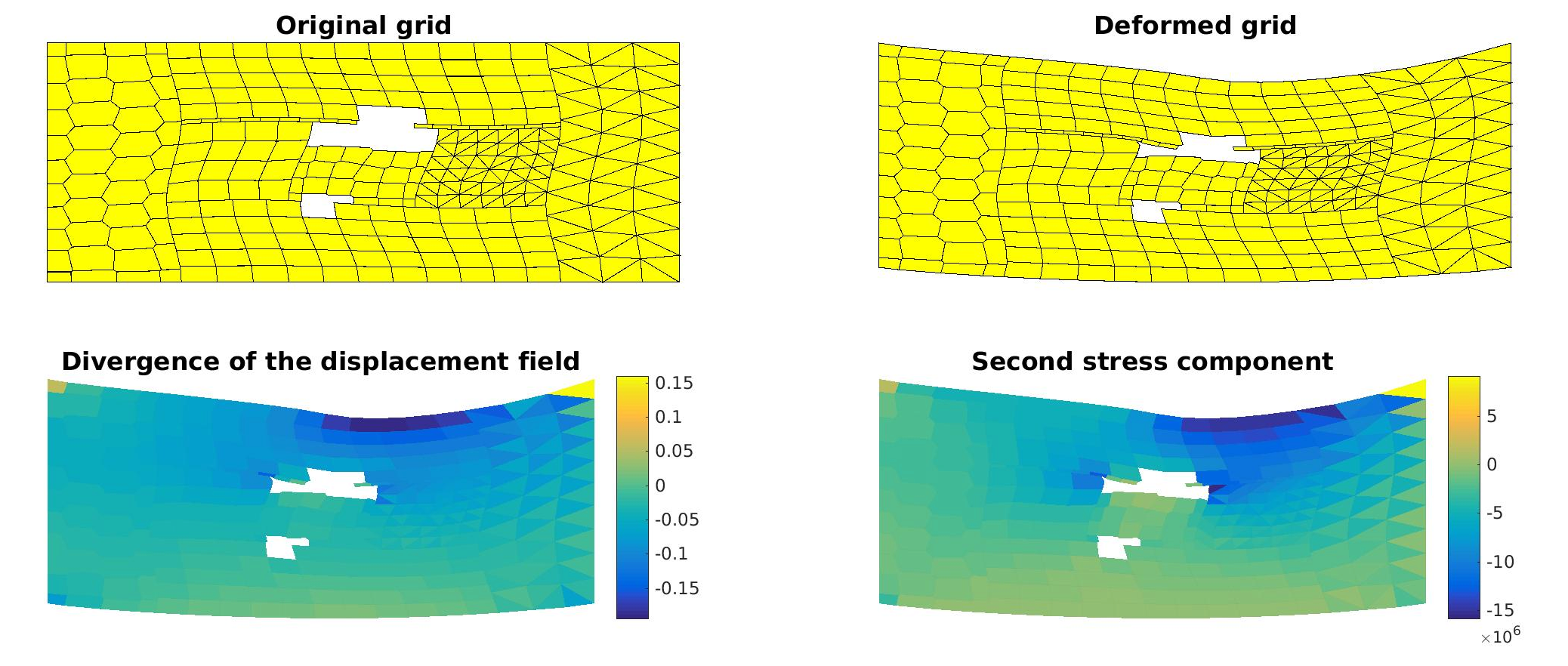
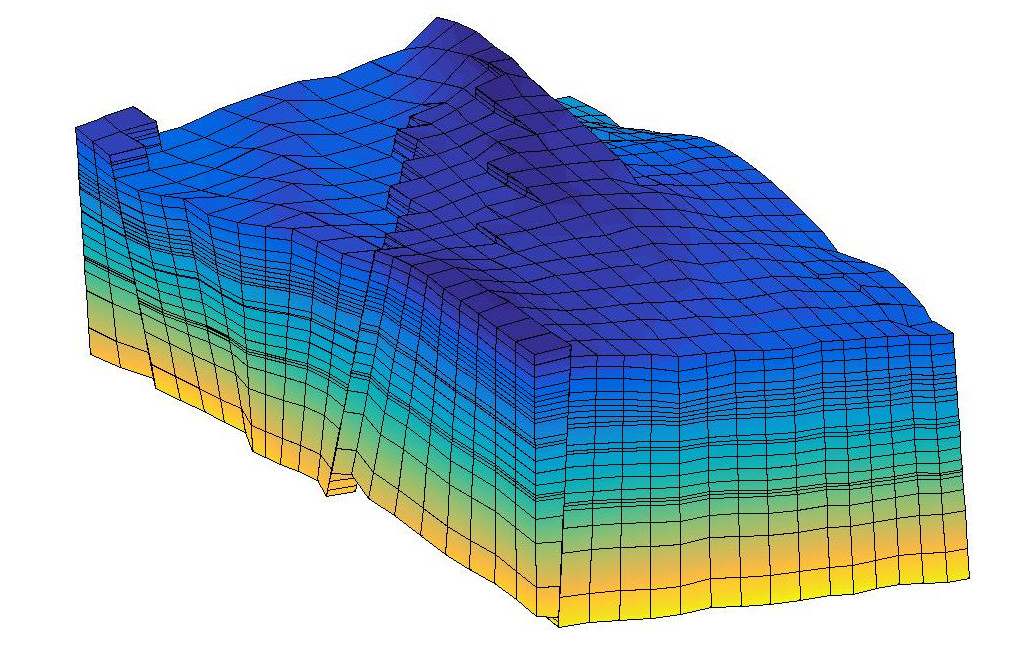
The virtual element method can be formulated as a finite element methods where the basis functions are neither given or computed. The method has the flexibility to handle irregular grid at the cost of an increased error in the energy norm, compared with classical finite element. We follow the implementation from Gain et al [1] and Beirao da Veiga [2].

In the examples, we consider several types of irregular grids which covers the main features of geological model such as irregular cell shapes, hanging nodes, high aspect ratios. The boundary conditions can either be set equal to a given force or as Dirichlet boundary conditions. The format supports gliding conditions in Cartesian directions. The illustrations below are compaction tests.

Simulation on a 2D grid containing the typical irregularities of geological models.

Third component of the stress field on a compaction test for Norne reservoir model

References

1. Gain L, Talischi C. and Paulino G.H., On the Virtual Element Method for three-dimensional linear elasticity problems on arbitrary polyhedral meshes Computer Methods in Applied Mechanics and Engineering, Vol. 282 2014, pp. 132-160, 2014
2. Beirao da Veiga L., Brezzi F., Marini L.D. and Russo A., The hitchhiker's guide to the virtual element method, Mathematical models and methods in applied sciences, Vol 24, No 08, pp 1541-1573, 2014
3. Andersen O., Nilsen H.M. and Raynaud X., On the use of the Virtual Element Method for geomechanics on reservoir grids, ArXiv e-prints 2016 https://arxiv.org/abs/1606.09508
4. Nilsen H., Nordbotten J. and Raynaud X., Comparison between cell-centered and nodal based discretization schemes for linear elasticity ArXiv e-prints 2016 https://arxiv.org/abs/1604.08410