Tutorials

Basic VEM tutorial In this example, we introduce the virtual element method (VEM) as implemented in MRST, and show how to set up the resulting solver and use it to solve two single-phase flow problems. The example discusses details such as inner products, degrees-of-freedom

2-phase transport in anisotropic domain In this example, we use the virtual element method (VEM) solver in MRST to solve a transport problem in which we inject a high-viscosity fluid in a reservoir with varying permeability, which is initially filled with a low-viscosity fluid. The domain is described by an unstructured, composite PEBI-grid (as generated by the upr module) representing a domain with three zones of different anisotropic permeability. To emphasize the importance of using a consistent discretization method for grids that are not K-orthogonal, we will compare the solution to the TPFA mehod.

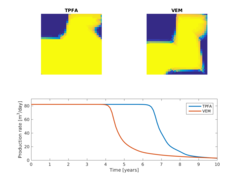
Description

This module has been developed by Øystein Klemetsdal as part of his master thesis [1], which was supervised by Xavier Raynaud from SINTEF ICT. Virtual element methods (VEM) constitute a unified framework for higher-order methods on general polygonal and polyhedral grids. The vem module can be used to solve general incompressible flow problems using first- and second-order VEM, with the possibility to choose different inner products. Applications of the methods to unstructured grids that adapt to geological features, as generated by the upr module, can be found in Klemetsdal et al. [2]. The paper also contains comparisons with TPFA and consistent solvers (mimetic, MPFA, NTPFA), which all are implemented in MRST.

Literature

1. Øystein Strengehagen Klemetsdal. The virtual element method as a common framework for finite element and finite difference methods - Numerical and theoretical analysis. NTNU, 2016.

2. Ø. S. Klemetsdal, R. L. Berge, K.-A. Lie, H. M. Nilsen, and O. Møyner. Unstructured gridding and consistent discretizations for reservoirs with faults and complex wells. SPE Reservoir Simulation Conference, Montgomery, Texas, USA, 20-22 February 2017.