|
HFM: Hierarchical Fracture Models
The hierarchical fracture module (HFM) utilises the hierarchical fracture modelling framework to simulate multiphase flow in naturally fractured reservoirs with multiple length scales. Also known as the embedded discrete fracture model, this method models fractures explicitly, as major fluid pathways, and benefits from independent definitions of the fracture and matrix grid. As a result, intricate fracture networks can be modelled easily, without the need for a complex underlying matrix grid that is conformal with each fracture. The module also extends the newly developed multiscale restriction smoothed basis (MsRSB) method to compute the flux field developed in a fractured reservoir. The multiscale approach of dealing with fractures is inspired by similar strategies developed for the multiscale finite volume (MSFV) method.
Tutorials
DescriptionThis module has been developed by Swej Shah from Delft University of Technology in collaboration with researchers at SINTEF. The module utilises a hierarchical fracture modelling (HFM) framework to simulate multiphase flow in naturally fractured reservoirs with multiple length scales. Literature
|
|||||||||||||||||||||

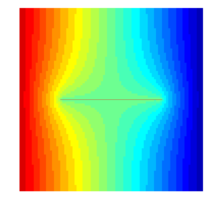

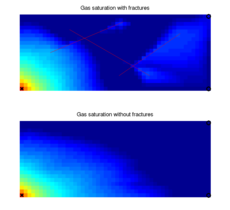
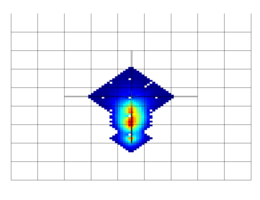
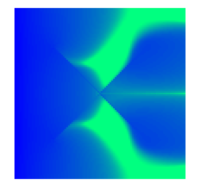
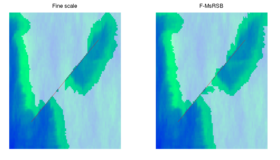

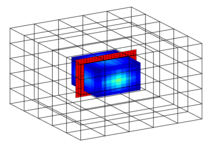 Water injection into 3D fractured medium
Water injection into 3D fractured medium