|
Forecasting long-term migration
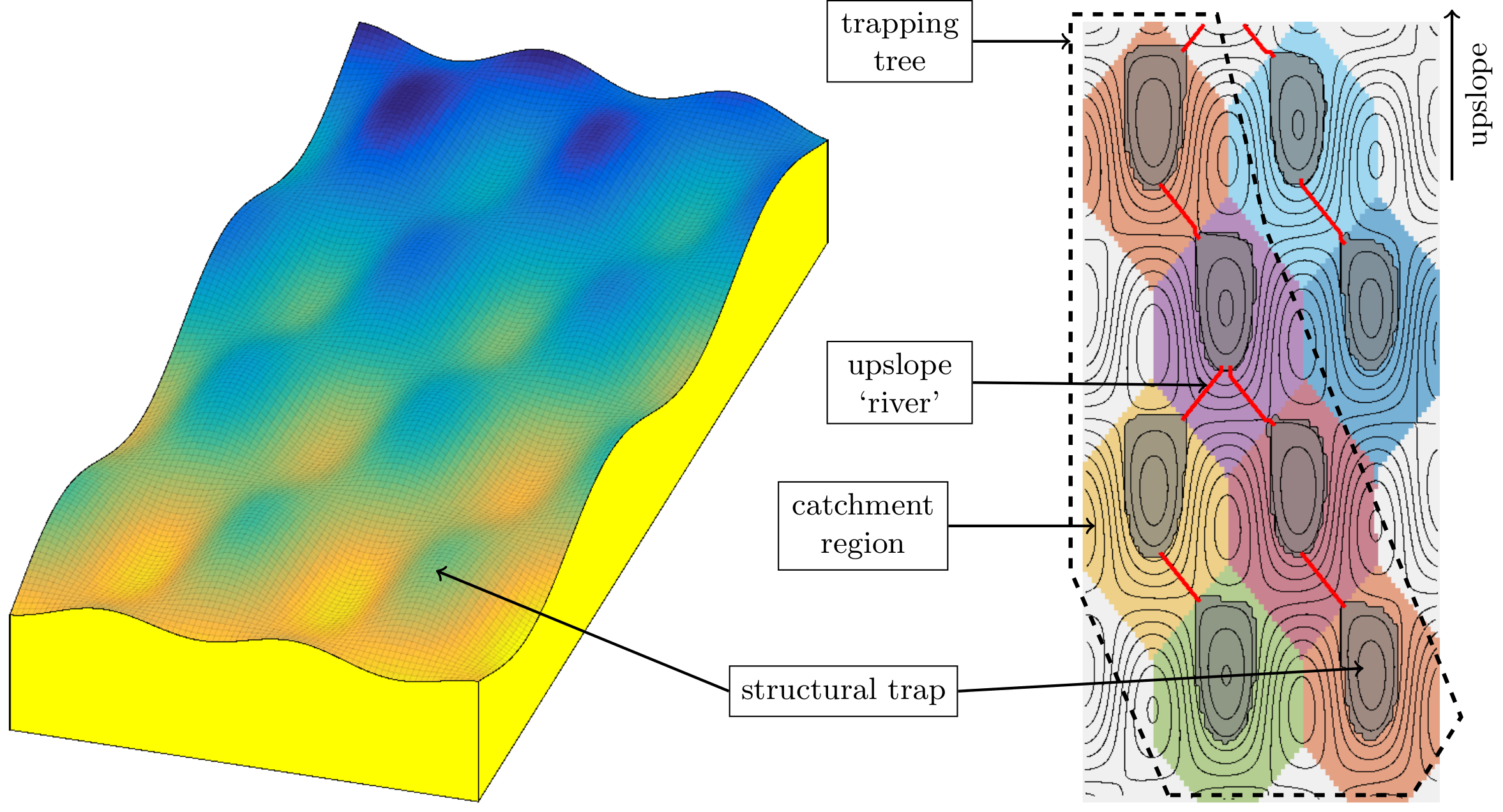
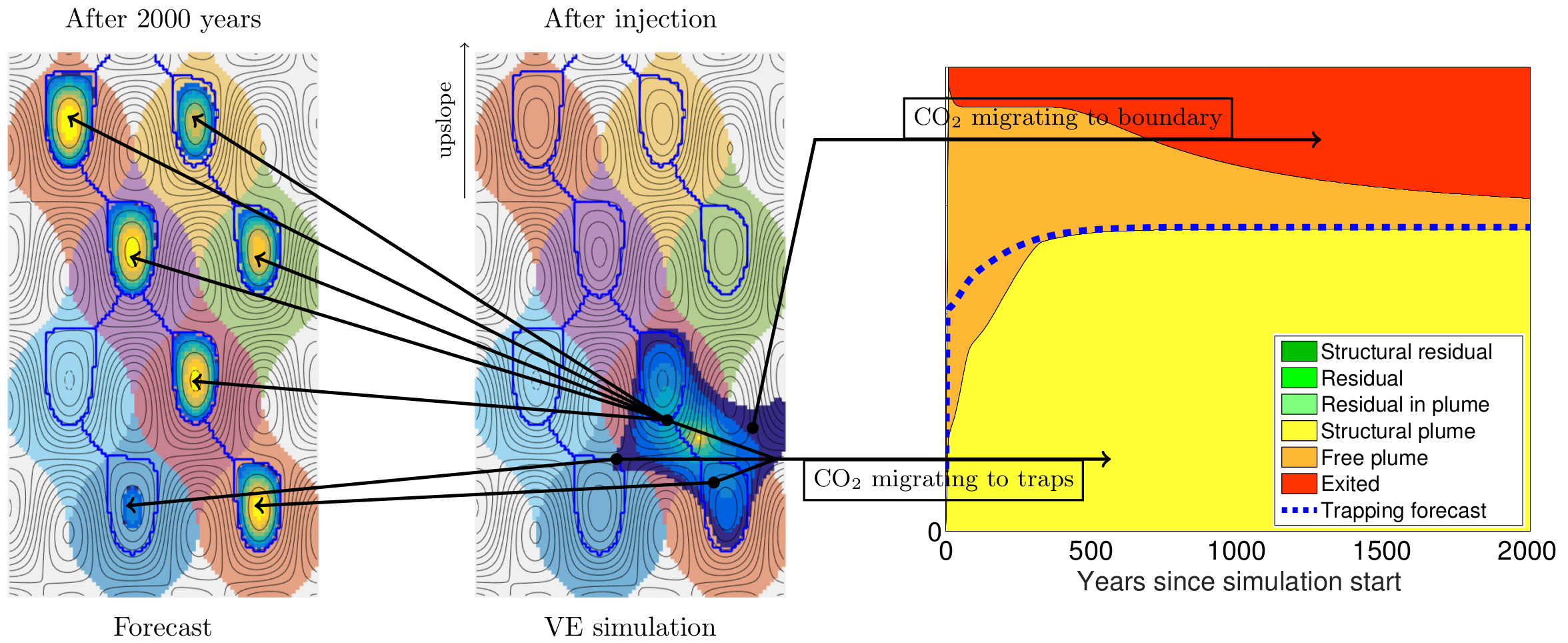
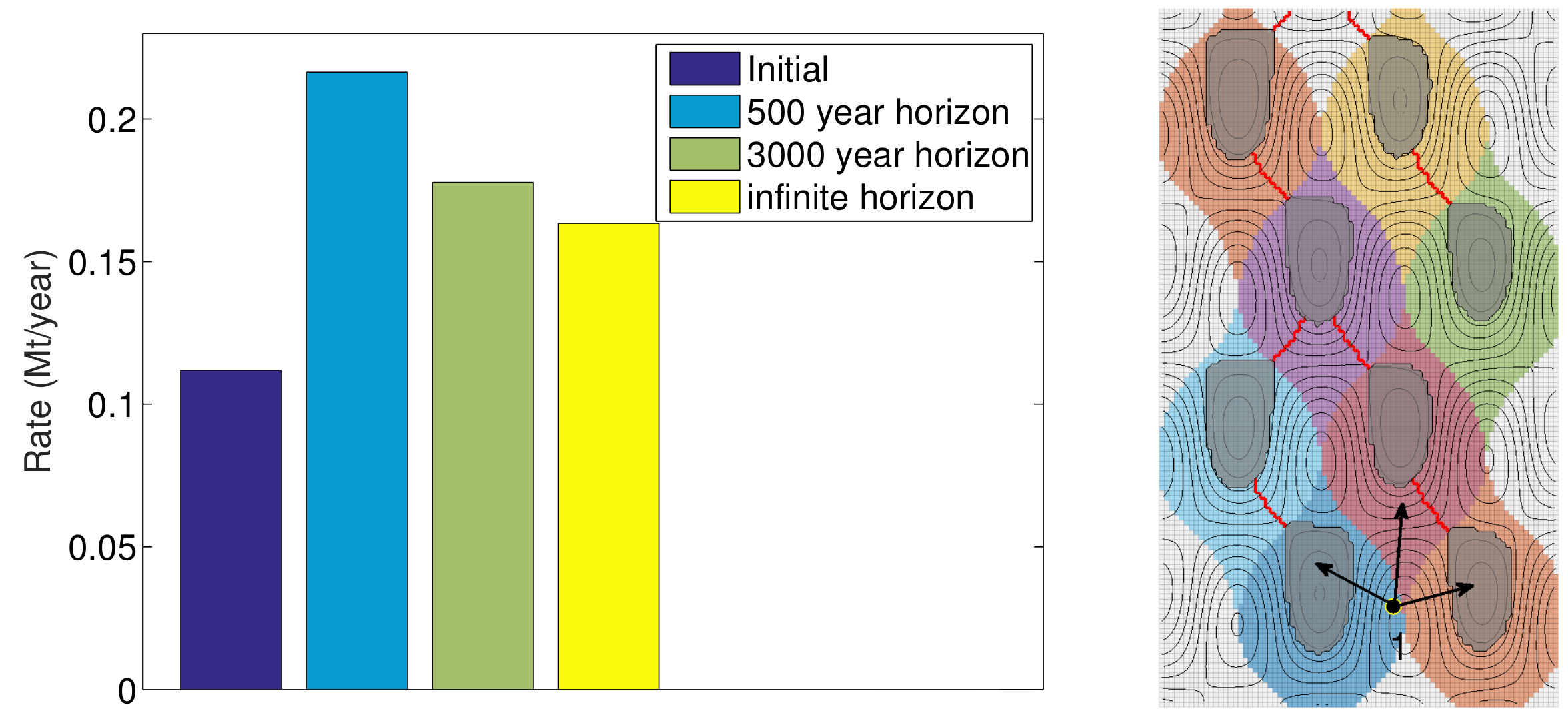
Capturing the long-term migration of CO2 within a large-scale saline aquifer may require the simulation of thousands or even millions of years. At such long time horizons, full numerical simulations based on the physical flow equations become practically impossible due to the computational cost. Rather than simulating for a finite number of years, we have implemented a forecasting algorithm that uses spill-point dynamics to predict the long-term migration of CO2, specifically how much will become trapped within the formation and how much is bound to leak out of the aquifer's open boundaries. Reducing the time it takes to perform a single simulation is particularly helpful when many simulations are required for the mathematical optimization of well injection rates. More details of the following example can be found in [1].
Literature
|
||||||