You are here:
MRST
/
Modules
/
MRST-co2lab
/
Depricated
/
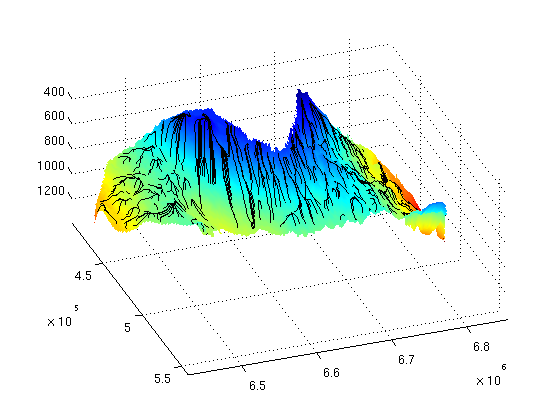
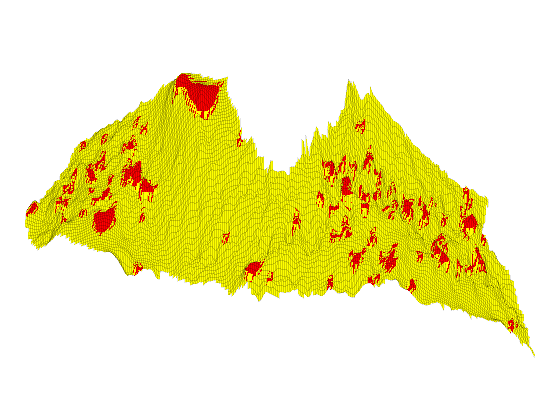
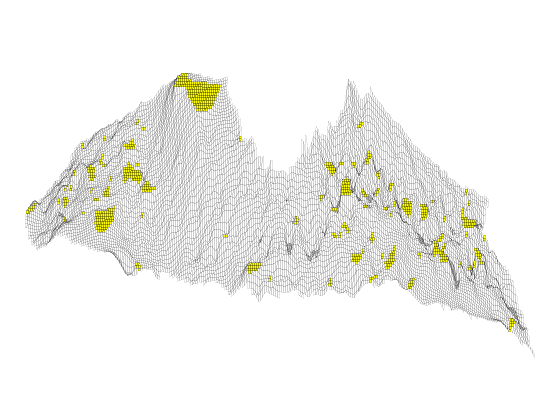
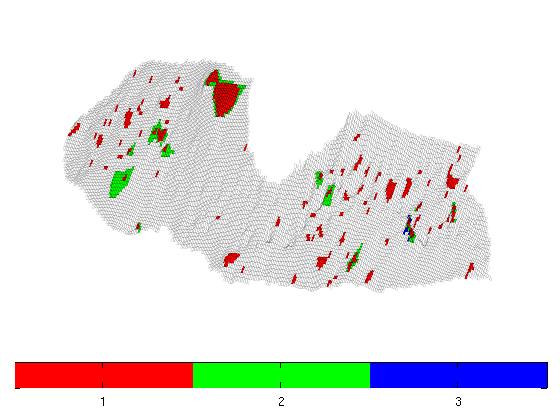
Investigation of Structural Trapping