You are here:
MRST
/
Modules
/
AD-FI old
/
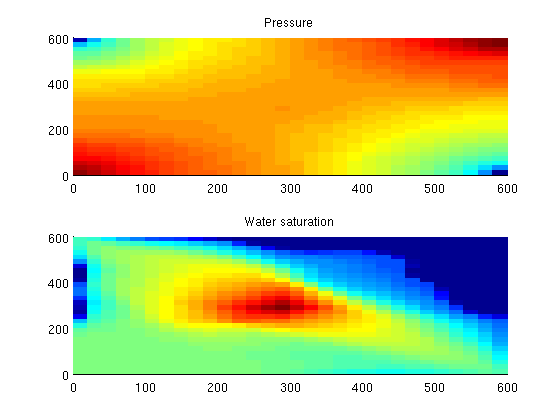
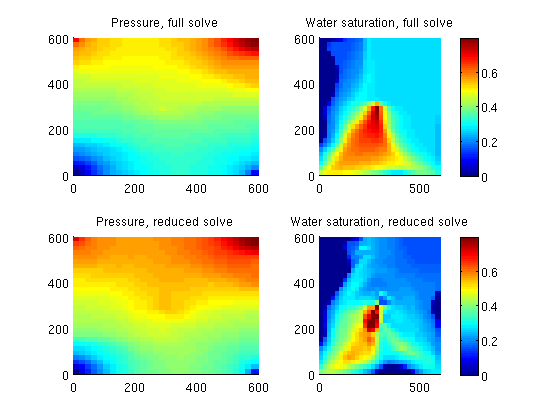
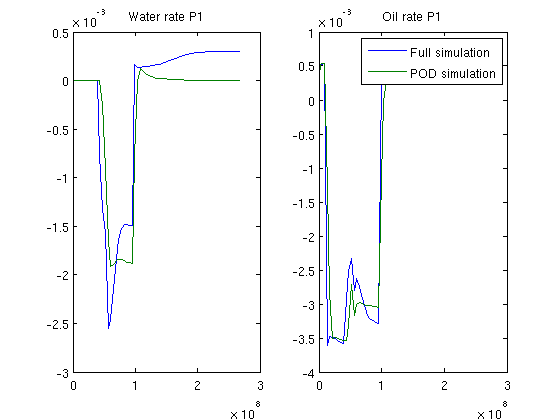
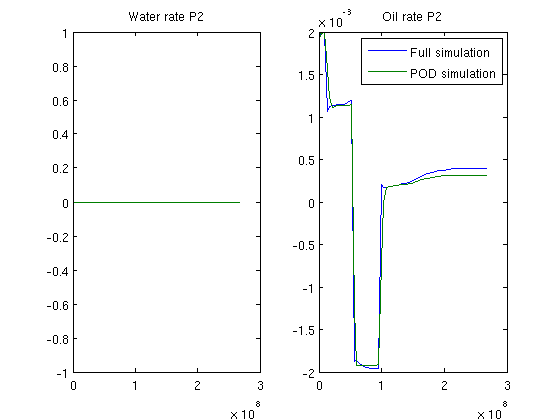
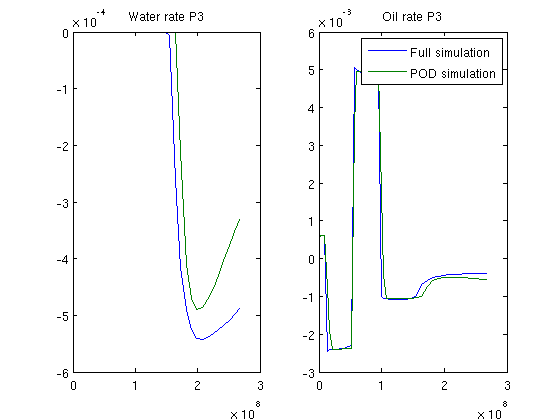
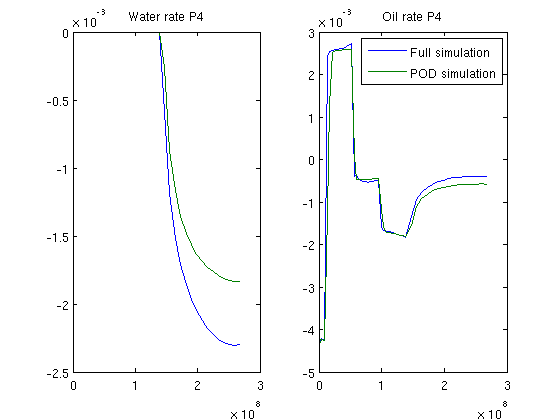
Proper Orthogonal Decomposition Example