You are here:
MRST
/
Modules
/
AD-FI old
/
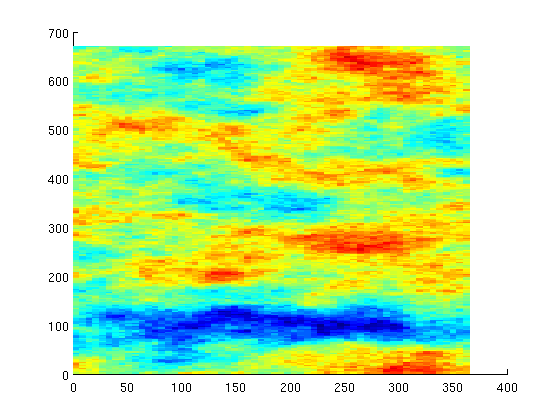
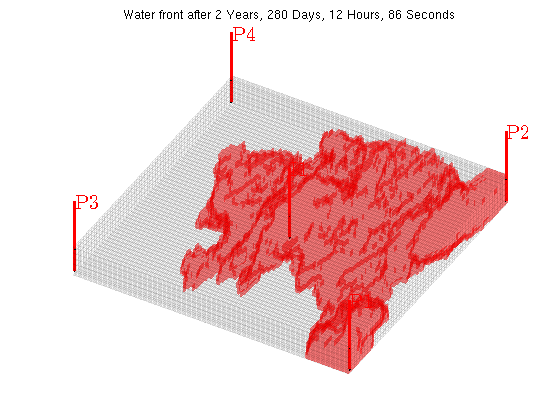
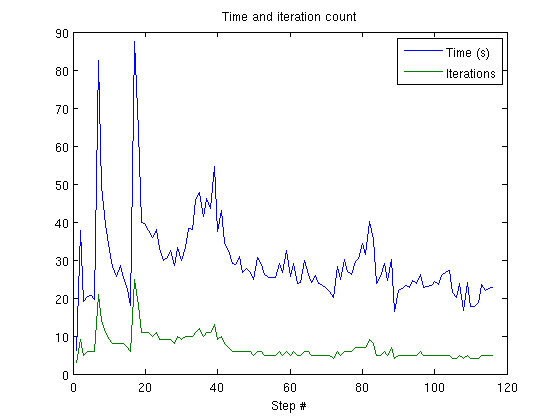
Fully implicit subset of SPE10 Model 2