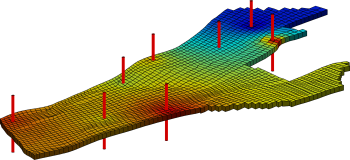
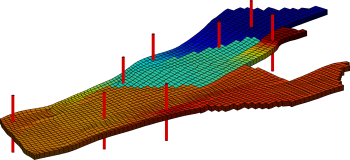
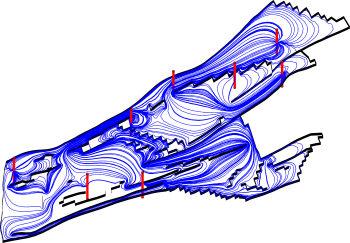
Faults affect the transmissibilities geometrically by introducing new cell-to-cell connections and by changing the contact areas between two cells that are juxtaposed over a fault surface. Similarly, the effective transmissibility is changed by fault-zone material interposed between cross-fault juxtaposed cells. To capture these effects, it is common to introduce transmissibility multipliers that account for the reduced or increased permeability for each cross-fault connection. These multipliers are highly grid dependent and strictly associated with a connection between two grid cells rather than with the fault itself. We have developed a new method that can correctly introduce the information inherent in fault multipliers into consistent schemes based on mixed, mimetic, and multipoint discretisations. The method implemented in MRST is described in more detail in a recent paper, H.M. Nilsen et al.: "Accurate modelling of faults by multipoint, mimetic, and mixed methods", SPE J., Vol. 17, No. 2, pp. 568-579, June 2012. DOI: 10.2118/149690-PA.

Example

We now demonstrate the effects of fault and shale layer barriers to flow on a real-field model from the Norwegian Sea. The barriers are represented in the model description as non-negative transmissibility multipliers less than unity. The figure below shows pressure field and corresponding streamlines resulting from a two-phase incompressible flow calculation in a 2D cartoon model derived from the full 3D model, with faults from the original modelled as internal boundaries, depicted in black. The flow is driven by a set of injection and production wells shown in red. The left plots show the results obtained when faults do not impose restrictions to flow, i.e., when all transmissibility multipliers equal unity. We can see that the pressure field is smooth and the streamlines pass through the faults. In the right plots, the faults are completely sealing, producing a discontinuous pressure field and streamline paths that are aligned with the faults.

Two-dimensional mock-up of a real-field model from the Norwegian Sea. The transmissibility multipliers can be used to adjust the impact of a fault from completely transparent (left) to fully sealing (right).