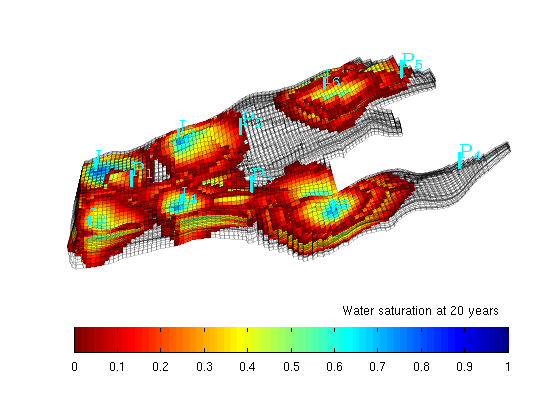
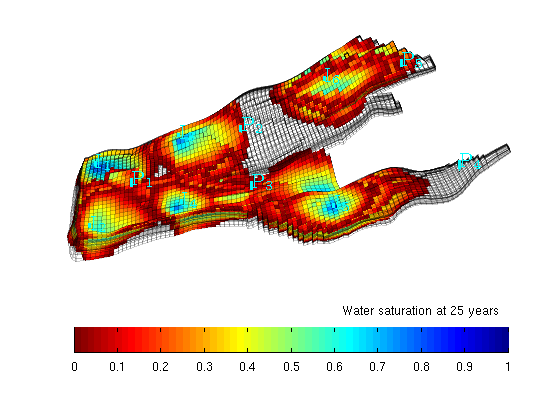
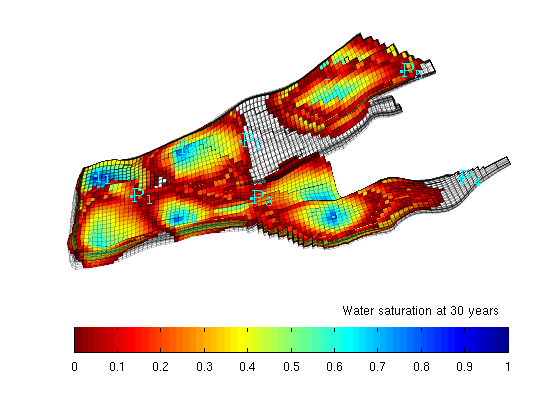
You are here:
MRST
/
Documentation
/
Tutorials
/
Real-Field Model: II