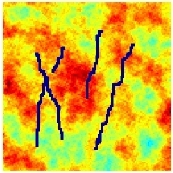
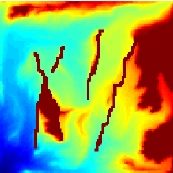
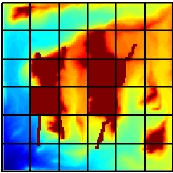
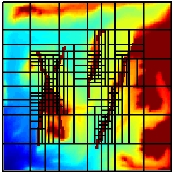
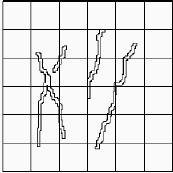
Use Grid Adaptivity to Increase Accuracy

Consider a quarter-five spot simulation defined over a heterogeneous permeablility field containing a set of barriers (with permability equal 1e-8 relative to the mean of the background permeability field). This example has been tailor-made to cause difficulties for the multiscale method.

To solve the flow problem, we employ the multiscale mixed finite-element method on a 6 x 6 coarse grid. Several of the grid cells are cut into two noncommunicating parts by the barriers. In the figure below, we see that the method fails to flood the corresponding cells properly. The reason is the following: when generating the multiscale basis functions, unit flow is forced through each cell. Therefore the velocity basis functions will model an unphysically high flow, for cells that are cut in two halves by a traversing barrier. As a result, the contribution from each such basis function becomes very small in the solution of the global flow problem on the coarse grid and the flux into the cell is zeroed out.

Permeability field with low-permeable barriers inposed on a lognormal background permeability

Reference saturation field computed using the velocity computed on the underlying fine grid

Saturation field computed using the multiscale velocity approximation

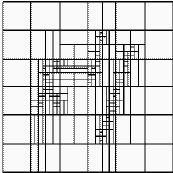
Improved accuracy can be obtained by the following two approaches:

1. Automatic hierarchical refinement based upon a given error indicator that measures the ratio of velocities over effective permeabilities.
2. Manually adding extra (irregular) coarse cells that contain the barriers.

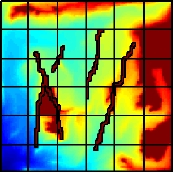
In the figure below we see that both approaches are able to reproduce the saturation with high accuracy. The best accuracy is obtained by adding barriers as coarse cells, even though this gives much fewer coarse cells than for the hierarchical approach.

If the barriers are removed, all three grids above give the same accuracy, indicating that the choice of coarse grid has little influence for a smoothly varying permeability field.

Automatic refinement, where the coarse grid is refined hierarchically around the flow barriers

Direct inclusion of the flow barriers as special blocks in the coarse grid

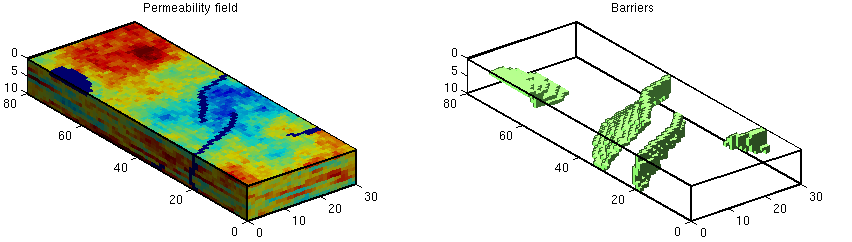
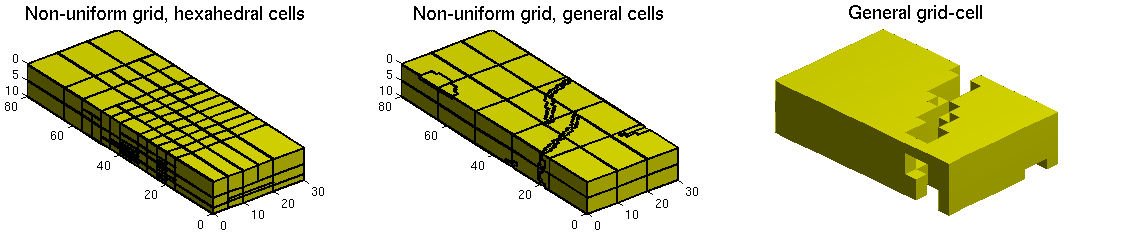
General Unstructured Coarse Grids in 3D

The two approaches introduced above can easily be extended to three spatial dimensions. In the figure below, we consider a 30 x 80 x 10 subsample of the Tarbert formation from the second SPE10 model, in which we have introduced a few low-permeable walls (1e-8 mD). To improve the accuracy of the multiscale solution, we can either perform a hierarchical refinement or search for connected cells of very low permeability and add them as extra coarse cells to a uniform background grid.

The upper row shows the case consists of the Tarbert formation from the SPE 10 test case (the 30 first layers) into which we have inserted low-permable flow barriers. The lower row shows a hierarchically refined grid and a grid where the low-permeable barriers are included as extra coarse blocks in a uniform coarse partition. The right plot shows one perticular coarse block that has been cut through by a flow barrier.

Multiscale Methods - Great Flexibility in Gridding

The examples above indicate the great flexibility inherent in the multiscale method: each coarse grid cell can be defined (almost) arbitarily as a connected set of fine-grid cells. For permeability fields with relatively smooth variation (but possibly with large variations), the multiscale method is not very sensitive to the shape and size of the cells in the coarse grid. For nonsmooth permeabilities, on the other hand, higher accuracy is obtained by a careful choice of the coarse grid.

References

1. J. E. Aarnes, S. Krogstad, and K.-A. Lie. A hierarchical multiscale method for two-phase flow based upon mixed finite elements and nonuniform coarse grids.  Multiscale Modelling and Simulation, Vol. 5, No. 2, pp. 337-363, 2006. DOI: 10.1137/050634566
2. J. E. Aarnes, S. Krogstad, and K.-A. Lie. Non-uniform coarse grids and multiscale mixed FEM. SIAM Geosciences 05, Avignon, France, June 7-10, 2005. (slides)