GeoScale - Direct Reservoir Simulation on Geocellular Models
|
Research areas
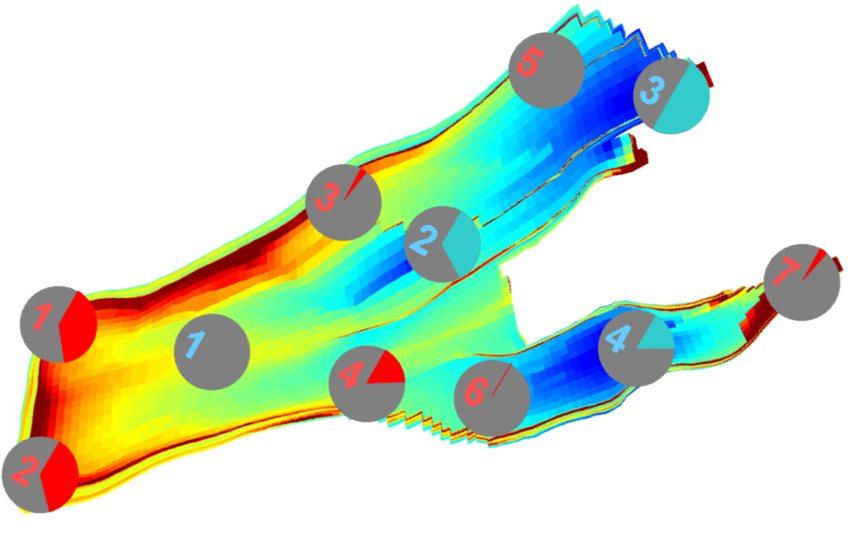
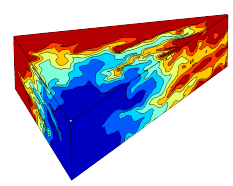
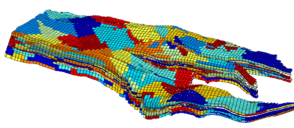
Here we present selected research areas from the GeoScale portfolio. More details about our research results can be found in our publications and presentations that are available online.
|
||||||||||||||||||