GeoScale - Direct Reservoir Simulation on Geocellular Models

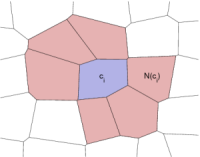
Coarsening by Amalgamation of Cells
Geological models are becoming increasingly large and detailed to account for heterogeneous structures on different spatial scales. To obtain simulation models that are computationally tractable, it is common to remove spatial detail from the geological description by upscaling. We have developed an algorithmic framework that consists of a set of modular components that can be combined in different ways to create flow-based coarse grids that are ideal for computing fluid transport. The fundamental characteristic of all algorithms is that coarse blocks are generated by amalgamating cells from the original fine grid, with a cell-wise indicator function guiding the amalgamation directions and the new grid resolution.

Assumptions:

  • a matching polyhedral grid with n cells c
  • a mapping N(c) between cell c and its nearest neighbours
  • a set of indicator functions I(c), each with a single value in cell c that can be used to locally control the amalgamation process

We seek a coarse grid that

  • adapts to flow patterns predicted by the indicator(s)
  • is formed by grouping cells into blocks
  • is described by a partition vector p with n elements, in which element number i assumes the value j if cell number i is part of block j

To coarsen the grid, we manipulate a set of partition vectors according to the following coarsening principles:

  • Minimize heterogeneity of flow field inside each grid block, e.g., by minimizing the variance of a flow indicator inside each block
  • Equilibrate indicator values over grid blocks (e.g., so that the volume of the block scales inversely with the magnitude of the local flow).
  • Keep block sizes within prescribed upper and lower bounds.
  • The internal block borders of any a priori partition that is marked as static should be preserved when grouping cells into blocks.

The general framework is implemented as a set of algorithmic primitives that create partition vectors (sources) and a set of primitives that manipulate them (filters):

  • Partition - take a grid and an indicator function (or some axuiliary information) as input and compute a partition as output. The partition vector can be constructed based on prescribed topology, on predefined block shapes, or as an segmentation of cells into bins according to a flow indicator.
  • Intersection - take one or more partition vectors as input and produce a new admissible partition vector as output, splitting multiply connected blocks into sets of singly connected cells.
  • Merging - merge blocks that are below a certain size (measured by a volume indicator. Each block is merged with the neighbouring block that has the closest indicator value.
  • Refinement - split blocks in which the accumulated indicator values exceed a prescribed threshold.

References:

  1. V. L. Hauge. Multiscale methods and flow-based gridding for flow and transport in porous media. Doctoral thesis, NTNU, 2010:181.
  2. K.-A. Lie and J. R. Natvig. Upgridding by amalgamation: Flow-adapted grids for multiscale simulations. SIAM Geosciences 2011, Long Beach, CA, USA, 21-24 March, 2011.
  


 

Example: Non-Uniform Coarsening

The first example of the amalgamation framework published by our group was the non-uniform coarsening method proposed by Aarnes, Efendiev, and Hauge [1]. The method consists of four steps, as illustrated in the figure to the right:

  1. Segment the velocity magnitude into 10 bins and construct coarse blocks as contiguous collections of cells belonging to the same bin.
  2. Merge blocks that have too small volumes with a neighbour.
  3. Split all blocks through which the total flow is too high.
  4. Repeat Step 2.

Later, the algorithm has been improved in several directions by using different neighbour definitions to grow blocks, combining flow adaption with a priori partitions, etc, as discussed by Hauge et al. [2].

  

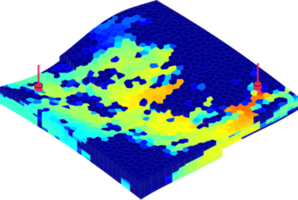
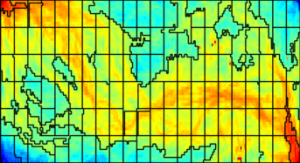
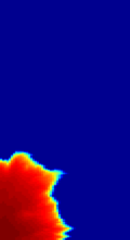
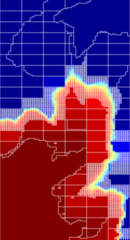
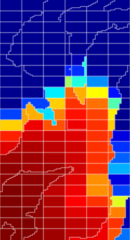
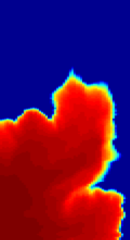
Flow-based coarsening generally gives improved accuracy in the computation of fluid transport, as shown in the figure below. We consider an extruded PEBI model with petrophysical parameters sampled from Layers 50-60 of the SPE10 benchmark and a diagonal displacement crated by placing an injector and a producer in opposite corners. The figure compares the saturation distribution after one pore-volume of water has been injected, simulated on three different grids. We observe that the METIS grid has too large blocks in the flow channel to capture the flow well, while the time-of-flight grid to a large degree matches the flow pattern from the original fine grid.

Original fine grid, 11 864 cells.

  

Coarsening based on time-of-flight, 127 cells.

  

Topological coarsening using METIS, 175 blocks.

 

References:

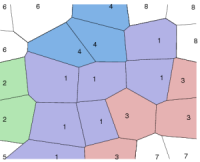
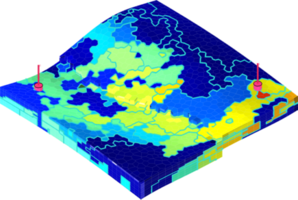
  1. J. E. Aarnes, V. L. Hauge, and Y. Efendiev. Coarsening of three-dimensional structured and unstructured grids for subsurface flow. Advances in Water Resources, Vol. 30, Issue 11, November 2007, pp. 2177-2193. DOI: 10.1016/j.advwatres.2007.04.007
  2. V. L. Hauge, K.-A. Lie, and J. R. Natvig. Flow-based coarsening for multiscale simulation of transport in porous media. Comput. Geosci.,  online first 2011. DOI: 10.1007/s10596-011-9230-x

Example: Hybrid Grids

The amalgamation framework is quite general and contains a large number of different coarsening methods as special cases. Each particular method can be expressed by combining the generic filters for merging and refining blocks with different a priori partitions and indicator functions. In the figure below, we show grids that are generated using a combination of structured topological and flow-based partitions.

Hybrid grid: topological partition combined with a flow-based partition with velocity as indicator.

  

Hybrid grid: topological partition combined with a flow-based partition with time-of-flight as indicator.

 

The coarsening can also be constrained to various geological features. In the figure below we use information of facies to constrain each coarse block so that it contains only one facies.

The distribution of facies in the domain which is considered as a static partition that is intersected with a standard flow-based partition based on e.g., flow magnitude or time-of-flight.

  

Cartesian fine grid.

  

PEBI fine grid.

 

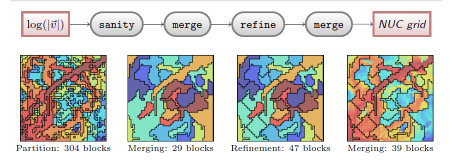
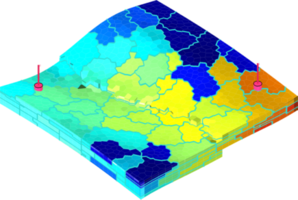
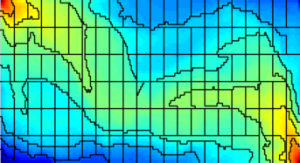
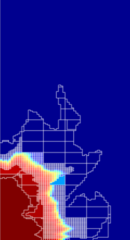
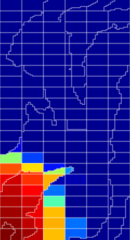
Example: Adaptive Grids

Because the all coarse grids created by agglomeration of cells from a fine grid are represented using a partition vector, it is (almost) straightforward to add dynamical adaptivity. We generate a coarse grid based on the time-of-flight indicator intersected with a uniform topological partitioning, as shown in the figure above. Local refinement, down to the resolution of the original grid, is added in regions near the displacement front. Cells that have time-of-flight values a certain fraction larger than those near the displacement front will likely belong to the unswept zone and are therefore merged into a single coarse block. Moreover, a band of blocks with intermediate resolution is kept ahead of the displacement front (measured in time-of-flight) to localise the search for regions that need to be refined in the next step and as a precaution when multiple time steps are computed without updating the grid. The figure below shows examples the adaptive grids for Layer 22 from the SPE10 model. For comparison, we also show the saturation profiles on the original and on a corresponding static coarse grid.

 

Examples of locally adapted grids for Layer 22 of the SPE10 model. The three plots to the left show saturation profiles after 0.1 pore volumes have been injected, whereas the rightmost plots show saturations at 0.5 PVI.

Published October 21, 2010

A portfolio of strategic research projects funded by the Research Council of Norway