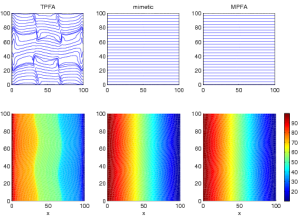
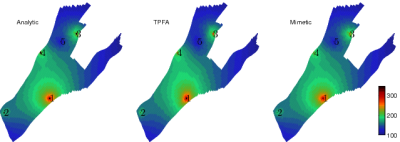
GeoScale - Direct Reservoir Simulation on Geocellular Models
You are here:
GeoScale
/
Research areas
/
Accurate Discretizations on Complex Grids
|
Accurate Discretizations on Complex Grids
|
||