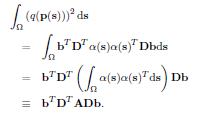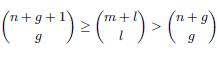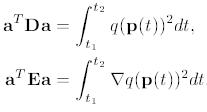|
Algebraic Geometry
Our focus is the use of knowledge from real algebraic geometry in Computer Aided Design (CAD). Rather than following the main trend within algebraic geometry of developing algorithms using exact arithmetic we use floating point arithmetic. The reason is that CAD-systems are based on floating point arithmetic like most industrial systems addressing geometry challenges.
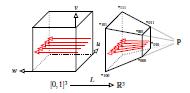
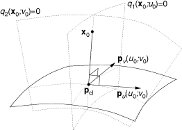
When implementing algorithms for CAD-systems it is desirable to both use parametric and implicit representations of curves and surfaces to make good algorithms. E.g., when intersecting two parametric curves of degree two or higher, p(s) and r(t), only using the parametric form will resulting in finding the zero set of two nonlinear equations in two variables: However, if one of the curves has an implicit representation qr(x,y)=0, we can directly express the problem as finding the zero set of one nonlinear equation in one variable qr(p(s))=0. Curves and surfaces in CAD-systems are represented as
The work on approximate implicitization in SINTEF started with the dissertation of Tor Dokken for the doctor philosophiae degree, Aspects of Intersection Algorithms and Approximation defended in 1997. Projects
Papers on approximate implicitization and real-time visualization of algebraic surface
|
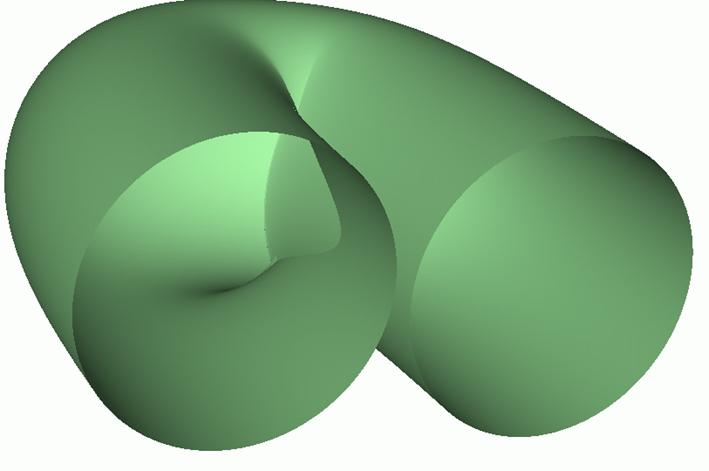
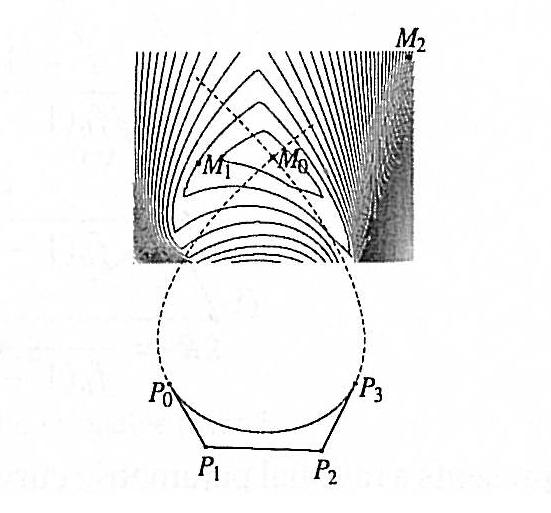
Real-time visualization of algebraic srufaces
Our work on Real-Time ray-casting of algebraic surfaces was inspired by a talk by Charles Loop on the use of algebraic curves for high quality visualization of fonts at the SIAM GD Conference in 2005. Returning from the conference Tor Dokken presented an approach to Johan S. Seland, resulting in the paper by Seland and Dokken in 2007. The cooperation was then extended to include Martin Reimers from the University of Oslo resulting in an improved approach presented in the paper by Reimer and Seland in 2008.
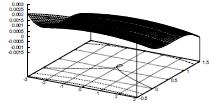
Approximate implicitization
After working with the development of intersection algorithms since 1979, Tor Dokken started to work on his PhD in 1992 addressing open question related to surface intersection algorithms. One idea was to find some way to find algebraic approximations to rational parametric surfaces. After a lot of experiments in Mathematica a new numerical stable approach with good approximation properties resulted. The results were made public available though the PhD dissertation in 1997, and the published in 2001. Approximate was the basis for the EU FET Open project GAIA (2000-2005) and the current Marie Curie Initial Training Network SAGA (2008-2012). | ||||||||||||||||||||||