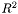PrParametrizeInt Class Reference

This class implements an algorithm for creating a parametrization in $R^2$ of the interior of a given embedding of a planar graph in 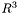$R^3$. More...

#include <PrParametrizeInt.h>

Inheritance diagram for PrParametrizeInt:

PrPrmEDDHLS PrPrmLeastSquare PrPrmMeanValue PrPrmShpPres PrPrmUniform List of all members.

Public Member Functions

 PrParametrizeInt ()
 Default constructor.
virtual ~PrParametrizeInt ()
 Empty default destructor.
void attach (boost::shared_ptr< PrOrganizedPoints > graph)
 Set the graph.
void setStartVectorKind (PrParamStartVector svtype=PrBARYCENTRE)
 Choose how to initialize the solution vector when running the internal solver.
void setBiCGTolerance (double tolerance=1.0e-6)
 Set tolerance for Bi-CGSTAB.
bool parametrize ()
 Parametrize the given planar graph.
bool parametrize3d (vector< int > &, vector< double > &)
 Parametrize the nodes of the 3D graph g_ except those with indices in "fixedPnts".
bool new_parametrize3d (vector< int > &, vector< double > &)
 Parametrize the nodes of the 3D graph g_ except those with indices in "fixedPnts".
void findFixedPntsFromXYZ (vector< int > &fixedPnts)
 This is a simple routine which finds the indices fixedPnts$[0...3]$ of the four vertices of the graph whose (x,y,z) points are the furthest in the directions (-1/-1/1), (1/1/1), (-1/1/-1), and (1/-1/-1) in that order.
void smooth (int nmb, vector< int > &fixedPnts)
 performs "nmb" Gauss-Seidel smoothing steps on the sphere
void computeWeights ()
 computes and stores the weights for each node

Protected Member Functions

int getNumIntNghrs (int i)
int getNumInt2Nghrs (int i, vector< int > &)
void findBarycentre (double &ucentre, double &vcentre)
bool isFixed (int, vector< int > &)
const vector< vector< double > > & getAllWeights () const
const vector< vector< int > > & getAllNeighbours () const

Protected Attributes

double tolerance_
PrParamStartVector startvectortype_
boost::shared_ptr< PrOrganizedPoints > g_
vector< int > neighbours_
vector< double > weights_
vector< vector< double > > allWeights_
vector< vector< int > > allNeighbours_

Detailed Description

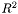This class implements an algorithm for creating a parametrization in $R^2$ of the interior of a given embedding of a planar graph in $R^3$.

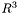The method is described in the paper: M. S. Floater, "Parametrization and smooth approximation of surface triangulations", CAGD 14 (1997), 231-250. The method sets u and v values to each interior node of the graph. The class PrParametrizeInt is an abstract base class. One must call one of its derived classes in order to choose a particular method of parametrization. We recommend the shape preserving parametrization implemented in PrPrmShpPres.

Definition at line 60 of file PrParametrizeInt.h.

Member Function Documentation

void PrParametrizeInt::setStartVectorKind ( PrParamStartVector  svtype = PrBARYCENTRE  )  [inline]

Choose how to initialize the solution vector when running the internal solver.

Choices are PrBARYCENTRE or PrFROMUV.

Definition at line 105 of file PrParametrizeInt.h.

References startvectortype_.

bool PrParametrizeInt::parametrize3d ( vector< int > &  ,
vector< double > &   
)

Parametrize the nodes of the 3D graph g_ except those with indices in "fixedPnts".

The parameterization is done in 3D and the result is returned as vector "uvw"

Definition at line 373 of file PrParametrizeInt.C.

References g_, getNumInt2Nghrs(), PrMatSparse::irow(), isFixed(), PrMatSparse::jcol(), neighbours_, PrBiCGStab::setMaxIterations(), PrBiCGStab::setTolerance(), PrBiCGStab::solve(), tolerance_, and weights_.

bool PrParametrizeInt::new_parametrize3d ( vector< int > &  ,
vector< double > &   
)

Parametrize the nodes of the 3D graph g_ except those with indices in "fixedPnts".

The parameterization is done in 3D and the result is returned as vector "uvw"

Definition at line 649 of file PrParametrizeInt.C.

References PrBiCGStab::converged(), g_, PrBiCGStab::getCPUTime(), PrBiCGStab::getItCount(), PrMatSparse::irow(), PrMatSparse::jcol(), PrMatSparse::matProd(), neighbours_, PrBiCGStab::setMaxIterations(), PrBiCGStab::setTolerance(), PrBiCGStab::solve(), tolerance_, and weights_.

void PrParametrizeInt::findFixedPntsFromXYZ ( vector< int > &  fixedPnts  ) 

This is a simple routine which finds the indices fixedPnts$[0...3]$ of the four vertices of the graph whose (x,y,z) points are the furthest in the directions (-1/-1/1), (1/1/1), (-1/1/-1), and (1/-1/-1) in that order.

The indices can be used as fixed points for parametrising in 3D.

Definition at line 798 of file PrParametrizeInt.C.

References g_.

The documentation for this class was generated from the following files:
Generated on Tue Jun 12 11:05:06 2007 for GoTools Parametrization Library by  doxygen 1.5.1