GeoScale - Direct Reservoir Simulation on Geocellular Models
|
SPE10
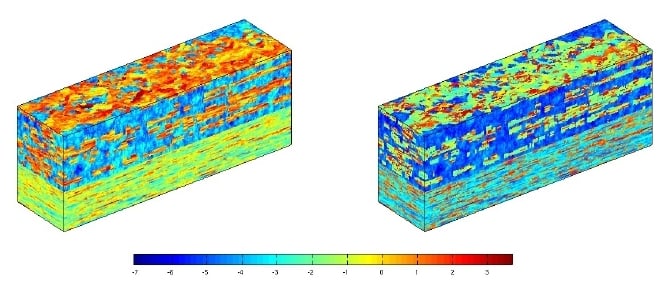
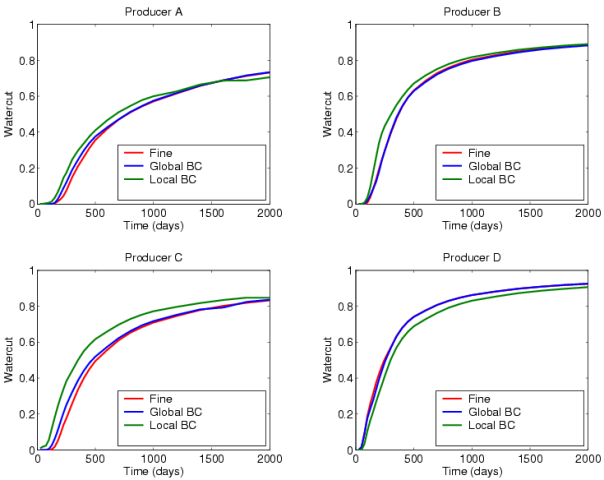
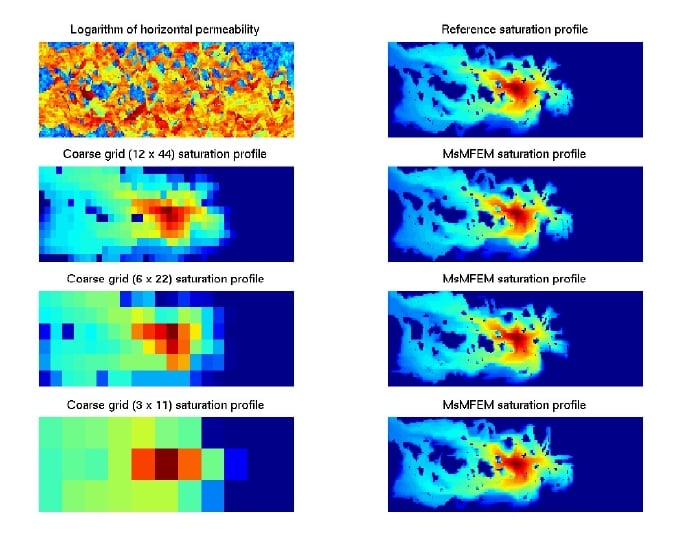
Multiscale methods are a promising alternative to upscaling and tend to give more accurate results than traditional nonpseudo and pseudo upscaling methods. Using our multiscale pressure solver in combination with a fast streamline method, we are able to match almost exactly the fine-grid production curves for the SPE10 benchmark. Beyond choosing an appropriate time step for the streamline simulator, our results involved no tuning of parameters.
|
|||