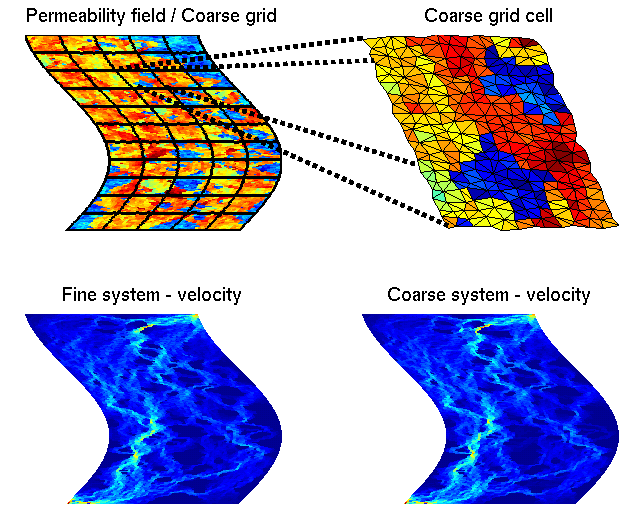
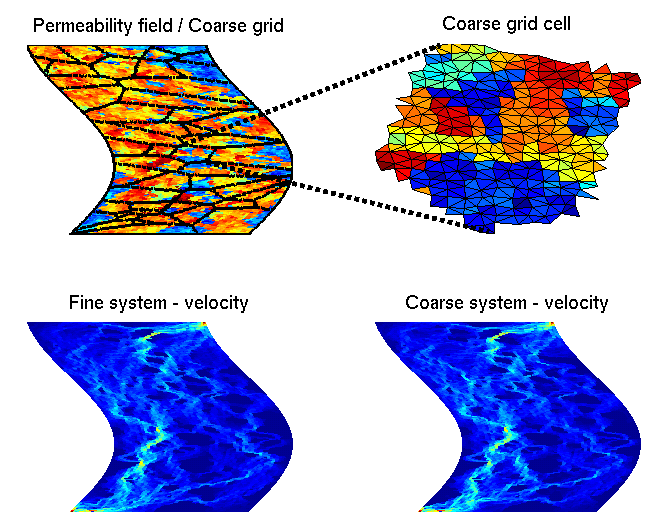
GeoScale - Direct Reservoir Simulation on Geocellular Models
You are here:
GeoScale
/
Research areas
/
MsMFEM
/
Multiscale Mixed Finite Elements on Triangular Grids