|
GAIA Home
The project "GAIA II - "Intersection algorithms for geometry based IT-applications using approximate algebraic methods" combines knowledge from Computer Aided Geometric Design (CAGD) and classical algebraic geometry to improve intersection algorithms for Computer Aided Design (CAD) types system.
The focus within the project is on:
At a first glance to calculate the intersection between curves or surfaces can seem simple. This is true for the intersection of e.g. two straight lines when they intersect transversally. For the intersection of two straight lines closed expressions for the intersection exist. However, if the lines are near parallel care has to be taken to implement a stable solution using floating point arithmetic. When we intersect two bi-cubic parametric surfaces the problem can be reduced to the zero set of a polynomial equation f(s,t)=0 of degree 54 in both variables, which by itself is a challenging problem. In industrial systems (e.g. CAD) double precision floating point arithmetic is used, thus introducing rounding errors. In CAD system there are tolerances defining when two points are to be regarded as the same point. This has also to be taken into consideration in CAD-related intersection algorithms. Low quality of intersection algorithms in CAD-systems imposes high costs on the product creation process in industry. To create a critical mass of researchers both addressing applied algebraic geometry and computer aided geometric design the project organized three workshops:
NOTE: There are images in the right margin of many of the GAIA II pages. If you do not see the images right of this text increase your window size. The pictures are often minimized versions. Click on the image to get the original size of the picture.
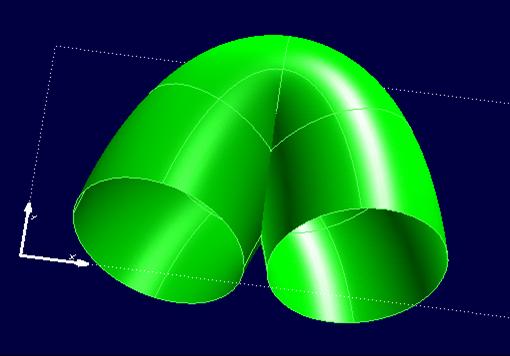
Examples of self-intersectioning surfaces in CAD. From the left a ruled draft surface, an offset surface and a pipe-surface. |
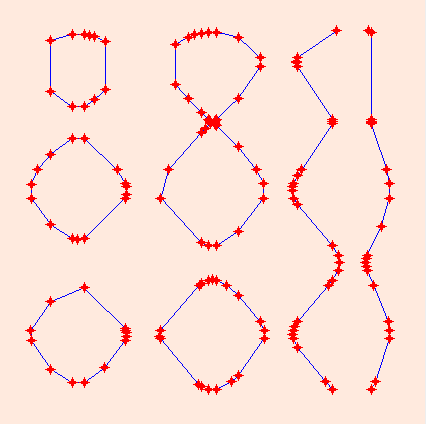
Examples of interesction produced by the recursive GAIA II intersection toolkit Trimming of self-intersecting tube surface. Intersection of a plane and a surface with many oscillations. The trace of the intersection in the parameter domain of the plane. Trace of the intersection in the domain of the oscillating surface.
| |