|
Multiscale Finite Volumes Module
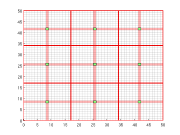
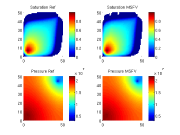
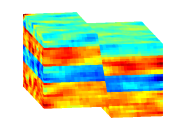
The module implements the operator forumulation of the multiscale finite-volume method developed by Jenny, Lee, Tchelepi and coworkers on unstructured grids in 3D. The MsFV method constructs a set of basis pressure functions which can be used to find a coarse pressure which can then be used to construct a fine scale pressure solution.
Tutorials
DescriptionThe MsFV method uses two coarse grids on top of a fine scale grid. A initial set of pressure basis functions taking heterogenities into account are constructed, which are then used to find a coarse scale system. Once a coarse scale solution has been obtained, the pressure basis functions can be used to extend the coarse scale solution into the fine scale. To improve the pressure solution, the pressure solver may be used in smoother cycles in a matter similar to multigrid solvers, or as a preconditioner for iterative methods such as GMRES converging to arbitrary precision. At any time during this process another set of basis functions, the flux basis functions, can be constructed, giving conservative flow at the fine scale. The basis functions can be reused in further calculations, giving a computationally inexpensive pressure updates for multiphase flow. This module is based on MRSTs existing TPFA solver. Literature
DownloadAs of the MRST 2012a release, this module is bundled with MRST Core in the standard release. |
||||||||