|
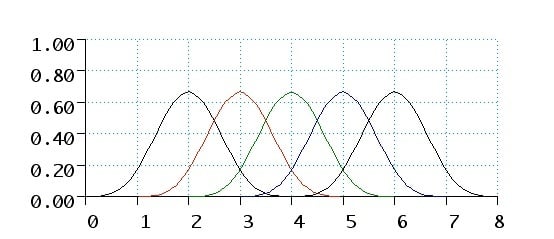
B-Splines
As a basis for the spline space of all polynomial spline functions of degree d on a knot vector {ti}, we use B-spline functions. A B-spline function is a polynomial spline function which is zero except on a small intervall [tj, tj+d+1]. The number of nonzero B-splines in a particular interval I = [tk, tk+1] is d+1, and their polynomial part on I form a basis of all d-degree polynomial functions on I. Therefore, when evaluating a spline function for a particular parameter value t, it suffices to evaluate the d+1 B-splines that are non-zero in t. The evaluation of B-splines is numerically stable and efficient, which is a major reason for why splines are so widely used in applied mathematics.
|
| |