|
MsRSB: Multiscale Restriction-Smoothed Basis Method
The Multiscale Restricted-Smoothing Basis (MsRSB) method is the current state-of-the-art within multiscale methods, originally developed by SINTEF and later implemented in the commercial INTERSECT MS SFI simulator.
MsRSB is very robust and versatile and can either be used as an approximate coarse-scale solver having mass-conservative subscale resolution, or as an iterative fine-scale solver that will provide mass-conservative solutions for any given tolerance. The performance of the method has been demonstrated on incompressible 2-phase flow, compressible black-oil models, as well as compositional models. It has also been demonstrated that the method can utilize combinations of multiple prolongation operators, e.g., corresponding to coarse grids with different resolutions, adapting to geological features, adapting to wells, or moving displacement fronts. At the moment, only parts of this functionality is available in the public version of the module.
Tutorials
Literature
|
||||||||||||

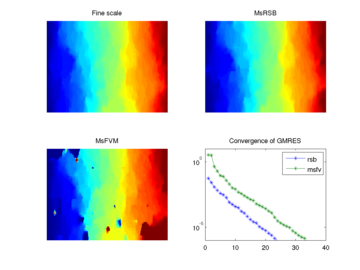 Introduction: SPE10 layer
Introduction: SPE10 layer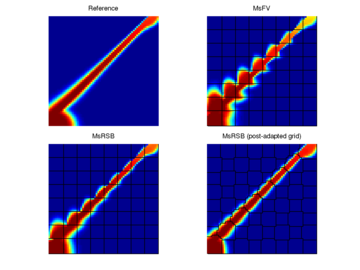 Grid adaption
Grid adaption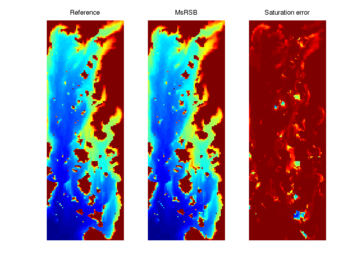 2-phase, Upper Ness
2-phase, Upper Ness Inactive cells
Inactive cells Bed model
Bed model Norne
Norne