Tutorials

Example 1 This example shows you how to partition rectangular 2D Cartesian grids, the relationship between cell and block numbers, and outlines the basics of the coarse-grid structure, including numbering of cells, faces, and node.		Example 2 We show partitions of grids representing more complex domains: a rectangular grid with a semi-circular cutout, a 3D cup-formed domain, a 2D Voronoi grid of rectangular domain with a quater-circle cutout, and a corner-point grid with a single fault.
Example 3 The example continues the discussion of the coarse-grid structure and shows how we can partition the coarse faces so that there are more than one face (connection) between neighboring coarse blocks.		Example 4 In this example, we take a closer look at partition vectors and discuss how different types of partitions can be combined into one.
Example 5 In this example, we use the function refineNearWell to make coarse grids with various types of near-well refinement. The examples uses both Cartesian and 2.5 D PEBI fine grids.		Example 6 We partition the Norne field uniformly in logical Cartesian space. Since the model contains many inactive cells, the initial partition must be postprocessed to ensure a contigous partition vector. We visualize some of the coarse blocks and show how they are connected with their neighbors.
Example 7 The example partitions the SAIGUP model uniformly in index space. Some of the blocks contain disconnected cells because of erosion, faults, etc. After these have been split, there is almost a factor 100 in size difference between the smallest and the largest coarse block. An extra processing step is included to ensure that coarse blocks have more uniform volumes.

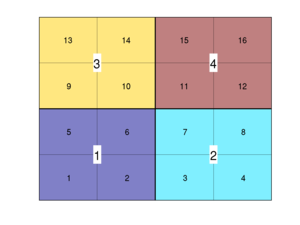
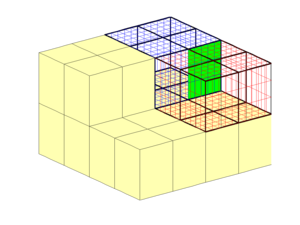
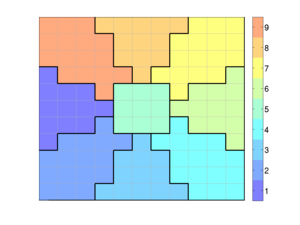
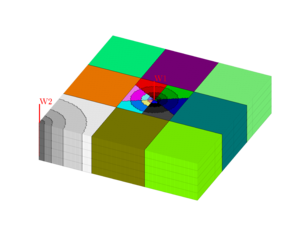
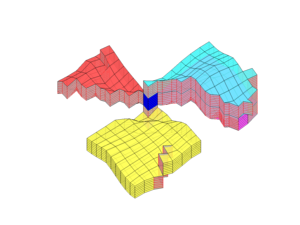
Description

In MRST, a coarse grid always refers to a grid that is defined as a partition of another grid, which is referred to as the 'fine' grid. The coarsegrid module defines a basic grid structure for such coarse grids and supplies simple tools for partitioning fine grids and turning these partitions into coarse grids that are compatible with the majority of the incompressible and compressible flow and transport solvers in MRST.

List of the main functions offered by the module:

• generateCoarseGrid - generate a coarse-grid data structure from a given fine grid and a partition vector
• partitionCartGrid - partition a logical n x m x k index set into a coarse N x M x K index set
• partitionLayers - partition grid uniformly in logical (I,J) direction, non-uniformly in K
• partitionMETIS - use the graph-partitioning software Metis (third party) to partition grid according to connection strengths
• partitionTensor - partition logically Cartesian grid into tensor product blocks
• partitionUI - partition a logically Cartesian grid using a load-balanced semi-uniform partition in each axial direction
• refineNearWell - partition a set of points based on proximity to a well point

In addition, the module offers a number of utility routines the operate on partitions or the coarse-grid structure

• compressPartition -- ensure that the partition vector is contigous
• processPartition -- ensure that the partition is connected, so that all cells inside the same block can be reached by traversing the graph defined by the cell faces of the block
• processFacePartition -- ensure that all coarse faces are connected collections of fine faces
• cellPartitionToFacePartition -- construct partition of all grid faces from cell partition
• subFaces -- extract fine-grid faces constituting individual coarse grid faces.

Literature

1. K.-A. Lie, S. Krogstad, I. S. Ligaarden, J. R. Natvig, H. M. Nilsen, and B. Skaflestad. Open source MATLAB implementation of consistent discretisations on complex grids. Comput. Geosci., Vol. 16, No. 2, pp. 297-322, 2012. DOI: 10.1007/s10596-011-9244-4